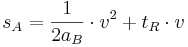Quadratische Funktionen - Anhalteweg: Unterschied zwischen den Versionen
(→Allgemein: f(x) = ax2 + bx) |
|||
| Zeile 32: | Zeile 32: | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=3| |
ARBEIT= | ARBEIT= | ||
#Experimentiere mit dem nachfolgenden Applet. | #Experimentiere mit dem nachfolgenden Applet. | ||
| Zeile 58: | Zeile 58: | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=4| |
ARBEIT= | ARBEIT= | ||
:Es passierte an einem sonnigen Tag, irgendwo auf einer idyllischen Straße durch einen lichten Wald. Herr Meier fuhr in seinem Cabriolet mit entspannten 80 km/h die kerzengerade Straße entlang, als plötzlich 60 m vor ihm ein Hirsch auf die Straße läuft... | :Es passierte an einem sonnigen Tag, irgendwo auf einer idyllischen Straße durch einen lichten Wald. Herr Meier fuhr in seinem Cabriolet mit entspannten 80 km/h die kerzengerade Straße entlang, als plötzlich 60 m vor ihm ein Hirsch auf die Straße läuft... | ||
| Zeile 91: | Zeile 91: | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=5| |
ARBEIT= | ARBEIT= | ||
:Untersuche an dem Applet rechts den '''Einfluss von b''' auf den Verlauf des Graphen. | :Untersuche an dem Applet rechts den '''Einfluss von b''' auf den Verlauf des Graphen. | ||
| Zeile 105: | Zeile 105: | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=6| |
ARBEIT= | ARBEIT= | ||
#Gibt es einen Zusammenhang zwischen dem blauen und grünen Graphen? Experimentiere erneut mit dem Applet und bestätige deine Vermutung. | #Gibt es einen Zusammenhang zwischen dem blauen und grünen Graphen? Experimentiere erneut mit dem Applet und bestätige deine Vermutung. | ||
Version vom 12. März 2010, 13:44 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3
Der Anhalteweg
Wir haben oben gesehen, dass man selbst bei relativ moderaten Geschwindigkeiten mit beachtlichen Bremswegen rechnen muss. Dabei blieb jedoch noch unberücksichtigt, dass der Anhalteweg nicht allein der reine Bremsweg ist, sondern dass zum Bremsweg auch noch der sogenannte Reaktionsweg hinzukommt.
Der Bremsweg ist derjenige Weg, den das Fahrzeug vom Beginn des Bremsvorgangs bis zum Stillstand zurücklegt. Er berücksichtigt also nicht, dass man nach dem Auftreten des Hindernisses eine gewisse Zeit (die Reaktionszeit') benötigt, bis man überhaupt reagieren kann und bremst. Reaktionsweg ist also die Strecke, die ein Fahrzeug in der Zeit zurücklegt, die der Fahrer braucht um eine Situation zu erkennen und mit dem Fuß anfängt das Bremspedal zu drücken. Die Geschwindigkeit ändert sich in dieser Zeit nicht.
|
Experimentieren mit einem Applet zum Anhalteweg
|
Im folgenden Applet ist der Zusammenhang zwischen Geschwindigkeit und Anhalteweg dargestellt worden. Mit Hilfe der Schieberegler können Geschwindigkeit v, Bremsbeschleunigung aB und Reaktionszeit tR variiert werden.
|
Den Einfluss der verschiedenen Faktoren auf die Länge des Anhalteweges kannst du auch mit diesem Applet untersuchen.
Allgemein: f(x) = ax2 + bx
| Die Funktionen, die wir in diesem Kapitel betrachtet haben, sind auch quadratische Funktionen. Sie haben den Funktionsterm ax2 + bx.
Wir lassen nun wie oben Aufgabe 3 den Wert für a gleich und verändern nur den Wert für b.
|
|

|
Nun kannst du wieder überprüfen, ob du alles verstanden hast! |
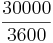 m in 1 Sekunde <=> 8,3 m in einer Sekunde
m in 1 Sekunde <=> 8,3 m in einer Sekunde