Quadratische Funktionen - Übungen 3: Unterschied zwischen den Versionen
(Original wieder hergestellt) |
(+weiterführende links) |
||
| Zeile 107: | Zeile 107: | ||
{{Autoren|[[Benutzer:Reinhard Schmidt|Reinhard Schmidt]], [[Benutzer:Christian Schmidt|Christian Schmidt]], [[Benutzer:Maria Eirich|Maria Eirich]], [[Benutzer:Andrea Schellmann|Andrea Schellmann]]}} | {{Autoren|[[Benutzer:Reinhard Schmidt|Reinhard Schmidt]], [[Benutzer:Christian Schmidt|Christian Schmidt]], [[Benutzer:Maria Eirich|Maria Eirich]], [[Benutzer:Andrea Schellmann|Andrea Schellmann]]}} | ||
| + | |||
| + | |||
| + | == Weiterführende Links == | ||
| + | [http://www.studienseminare-ge-gym.nrw.de/K/riemer/mathematik/publikationen/videoanalyse/index-videoanalyse.htm Videoanalyse: Geschwindigkeit und Bremswege] von [http://www.riemer-koeln.de/joomla/ Wolfgang Riemer] | ||
Version vom 31. Mai 2010, 10:31 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3
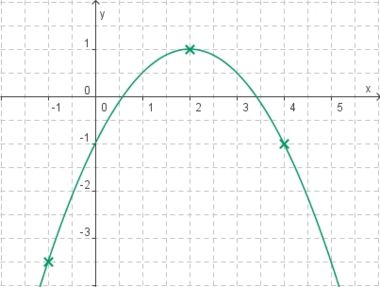
Aufgabe 1: Funktionsterm finden
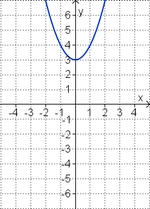
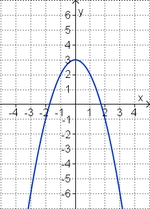
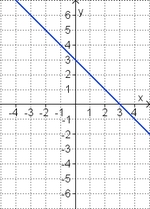
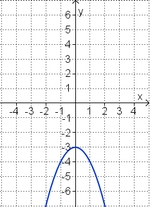
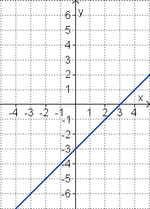
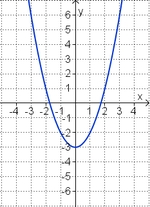
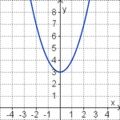
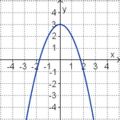
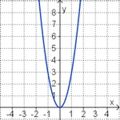
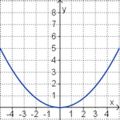
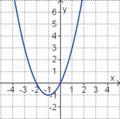
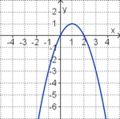
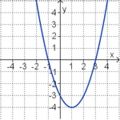
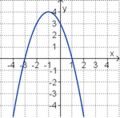
Aufgabe 2: Term und Graph zuordnen Ordne den Funktionsgraphen den richtigen Term zu.
Aufgabe 3: Multiple Choice Kreuze jeweils alle richtigen Aussagen an. f(x) = –2x2 + 3x – 4 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-6] liegt auf dem Graphen.) (Der Punkt [1|1] liegt nicht auf dem Graphen.)
Aufgabe 4: Memo-Quiz Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).
*Zusatz: Weitere interaktive Übungen
Weiterführende LinksVideoanalyse: Geschwindigkeit und Bremswege von Wolfgang Riemer |