Sek2Uni: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(→Analyse des Verhaltens einer gegebenen Funktion) |
(→Analyse des Verhaltens einer gegebenen Funktion) |
||
| Zeile 12: | Zeile 12: | ||
*sehr viel kleiner als die Lichtgeschwindigkeit <math>c</math> | *sehr viel kleiner als die Lichtgeschwindigkeit <math>c</math> | ||
*sehr nahe der Lichtgeschwindigkeit <math>c</math> | *sehr nahe der Lichtgeschwindigkeit <math>c</math> | ||
| − | sind? Methoden zur Analyse | + | sind? Stelle insbesondere Näherungsformeln für die beiden Grenzfälle auf! |
| + | Benutze die dir bekannten Methoden zur Analyse einer Funktion, wie | ||
*Plotten des Funktionsgraphen und elementare Analyse des Funktionsterms, um das Aussehen des Graphen qualitativ zu erklären, | *Plotten des Funktionsgraphen und elementare Analyse des Funktionsterms, um das Aussehen des Graphen qualitativ zu erklären, | ||
| − | *Methoden der Kurvendiskussion (Nullstellen, Extremstellen, Wendestellen,...) und | + | *Methoden der Kurvendiskussion (Definitionsmenge, Nullstellen, Extremstellen, Wendestellen,... ermitteln) und |
*Reihenentwicklung bzw. verwandte Näherungsmethoden. | *Reihenentwicklung bzw. verwandte Näherungsmethoden. | ||
| − | <font color="#000099">Anmerkung: Die Funktion <math>\gamma(v)</math> tritt in vielen Beziehungen der speziellen Relativitätstheorie auf. So stellt sie beispielweise den Faktor dar, um den bewegte Uhren langsamer gehen als ruhende und um den Objekte in Bewegungsrichtung verkürzt sind. Im Zwillingsparadoxon gibt sie den Faktor an, um die die von den Zwillingen gemessenen Zeinintervalle voneinander abweichen. Die berühmte Beziehung <math>E=mc^2</math> verallgemeinert sich für einen bewegten Körper zu <math>E=\gamma(v)mc^2</math>.</font> | + | <blockquote><font color="#000099">Anmerkung: Die Funktion <math>\gamma(v)</math> tritt in vielen Beziehungen der speziellen Relativitätstheorie auf. So stellt sie beispielweise den Faktor dar, um den bewegte Uhren langsamer gehen als ruhende und um den Objekte in Bewegungsrichtung verkürzt sind. Im Zwillingsparadoxon gibt sie den Faktor an, um die die von den Zwillingen gemessenen Zeinintervalle voneinander abweichen. Die berühmte Beziehung <math>E=mc^2</math> verallgemeinert sich für einen bewegten Körper zu <math>E=\gamma(v)mc^2</math>.</font></blockquote> |
== xxx == | == xxx == | ||
Version vom 4. August 2008, 11:13 Uhr
Lernpfad zur Schnittstelle Sekundarstufe 2 - Universität
Inhaltsverzeichnis |
Zum Stoff der Sek 2
Analyse des Verhaltens einer gegebenen Funktion
Wie verhält sich die Funktion
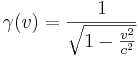
für Geschwindigkeiten 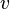 , die
, die
- sehr viel kleiner als die Lichtgeschwindigkeit

- sehr nahe der Lichtgeschwindigkeit

sind? Stelle insbesondere Näherungsformeln für die beiden Grenzfälle auf! Benutze die dir bekannten Methoden zur Analyse einer Funktion, wie
- Plotten des Funktionsgraphen und elementare Analyse des Funktionsterms, um das Aussehen des Graphen qualitativ zu erklären,
- Methoden der Kurvendiskussion (Definitionsmenge, Nullstellen, Extremstellen, Wendestellen,... ermitteln) und
- Reihenentwicklung bzw. verwandte Näherungsmethoden.
Anmerkung: Die Funktiontritt in vielen Beziehungen der speziellen Relativitätstheorie auf. So stellt sie beispielweise den Faktor dar, um den bewegte Uhren langsamer gehen als ruhende und um den Objekte in Bewegungsrichtung verkürzt sind. Im Zwillingsparadoxon gibt sie den Faktor an, um die die von den Zwillingen gemessenen Zeinintervalle voneinander abweichen. Die berühmte Beziehung
verallgemeinert sich für einen bewegten Körper zu
.
xxx
Text
xxx
Text
Weiterführendes
xxx
Text
xxx
Text
xxx
Text

