Version vom 2. Oktober 2008, 12:38 Uhr

Dieser Lernpfad bietet einen Einstieg das wichtige Thema "Quadratische Funktionen". Die Einführung in das Thema soll am Beispiel des Bremsweges eines Autos, genauer gesagt anhand des Zusammenhangs zwischen der Geschwindigkeit eines Autos und der Länge seines Bremsweges erfolgen. Der Lernpfand enthält eine Reihe von interaktiven Übungen, insbesondere auch einige GeoGebra-Applets.

Kompetenzen Das kannst du schon: Bei linearen Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln Parameter variieren und die Auswirkung dieser Variation beschreiben (Handhabung von GeoGebra) von der graphischen Darstellung unmittelbar auf die Darstellung als Formel schließen Eigenschaften linearer Funktionen aus der Termdarstellung ablesen und sie begründen Das kannst du lernen: Übersetzen von einer Realsituation in ein mathematisches Modell Parabeln als Graphen quadratischer Funktionen identifizieren Bei quad. Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln Parameter variieren und die Auswirkung dieser Variation beschreiben

Graphische Darstellung

Die Polizei hat Messungen durchgeführt, um den Zusammenhang zwischen der Geschwindigkeit eines Autos und seinem Bremsweg zu erkunden. Klar ist: Je schneller eine Auto fährt, desto länger ist sein Bremsweg. Aber ist das wirklich so einfach...?

Du kannst den Zusammenhang selbst untersuchen. Hier sind die Daten, die die Polizei gesammelt hat:

Aufgabe   a) Stelle die Daten aus der Tabelle in einem Koordinatensystem dar. b) Verbinde die Punkte zu einem Funktionsgraphen (der keine Ecken haben sollte.) c) Ermittle anhand des Graphen einen Schätzwert für den Bremsweg bei 70 km/h.    Lösung:

Der Funktionsterm

[Hier muss noch ein Text hin, der die Schüler zur Formel s=0,01*v^2 führt.]

Aufgabe   a) Hinter den Daten der Wertetabelle steckt ein Muster. Versuche eine Formel zu finden, mit deren Hilfe man aus der Geschwindigkeit den Bremsweg berechnen kann. b) In der Fahrschule lernt man: BW = v/10 mal v/10 (Bremsweg = Geschwindigkeit durch 10 mal Geschwindigkeit durch 10). Vergleiche diese Formel mit der von dir in a) gefundenen Formel.

Unfallprotokoll

Im ruhigen Dörfchen Niederbremsbach hat Herr Mütze ein kleines Mädchen angefahren, das ihrem auf die Straße rollenden Ball hinterher lief. Obwohl das Mädchen mit dem Schrecken davonkam, soll nun geklärt werden, ob sich Herr Mütze an die Geschwindigkeitsbegrenzung von 50 km/h gehalten hatte. Dem Unfallprotokoll ist zu entnehmen, dass Herr Mütze einen Bremsweg von 30,25 Metern hatte.

Aufgabe   a) Entscheide, ob sich Herr Mütze an die Geschwindigkeitsbegrenzung gehalten hatte. b) Berechne die Geschwindigkeit, die zu einem Bremsweg von 30,25 Metern führt.

Unterschiedliche Straßenverhältnisse

Bisher waren wir davon ausgegangen, dass die Länge des Bremsweges lediglich von der Geschwindigkeit abhängt. Das ist natürlich Unsinn. Bei gleicher Geschwindigkeit hat ein alter LKW auf schneeglatter Fahrbahn selbstverständlich einen ungleich längeren Bremsweg als ein neuer Kleinwagen auf einer trockenen und sauberen Straße. Diese Einflüsse kommen in der sogenannten "Bremsverzögerung" zum Ausdruck. Die Bremsverzögerung gibt an, wie stark ein Fahrzeug abgebremst wird: Eine hohe Bremsverzögerung spricht also für einen kurzen Bremsweg.

In einer Formel für den Bremsweg sollte also nicht nur die Geschwindigkeit, sondern auch die Bremsverzögerung berücksichtigt werden. In lehrbüchern findet man die Formel:
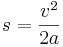                  (s = Bremsweg in m, v = Geschwindigkeit in m/s und a = Bremsverzögerung in m/s²).

In dem folgenden GeoGebra-Applet kann der Bremsweg variiert werden.

Aufgabe   Wie muss a gewählt werden, damit ... a) ...bei der Geschwindigkeit von 74 km/h der Bremsweg 65 m lang ist? b) ...bei der Geschwindigkeit von 74 km/h der Bremsweg 37 m lang ist? c) ...bei der Geschwindigkeit von 51 km/h der Bremsweg 58 m lang ist?

Die Funktionen, die wir bis jetzt betrachtet haben, weisen eine Gemeinsamkeit auf: Ihr Funktionsterm hat die Form Zahl mal Variable im Quadrat. Sie zählen daher zu den quadratischen Funktionen. Die Graphen quadratischer Funktionen unterscheiden sich stark von den Graphen linearer Funktionen (welches ja bekanntlich Geraden sind).

Merke: Die Graphen von Funktionen mit der Funktionsgleichung f(x)=ax² heißen Parabeln. Für a>0 gilt: Je größer a ist, desto steiler ist die Parabel.

Der Anhalteweg

Wir haben oben gesehen, dass man selbst bei relativ moderaten Geschwindigkeiten mit beachtlichen Bremswegen rechnen muss. Dabei blieb jedoch noch unberücksichtigt, dass der Anhalteweg nicht allein der reine Bremsweg ist, sondern dass zum Bremsweg auch noch der sogenannte Reaktionsweg hinzukommt.
Der Bremsweg ist derjenige Weg, den das Fahrzeug vom Beginn des Bremsvorgangs bis zum Stillstand zurücklegt. Er berücksichtigt also nicht, dass man nach dem Auftreten des Hindernisses eine gewisse Zeit (die Reaktionszeit) benötigt, bis man überhaupt reagieren kann und bremst. Der Weg, den das Fahrzeug angesichts der Reaktionszeit noch ungebremst zurücklegt, nennt man Reaktionsweg.

Aufgabe   a) Man kann davon ausgehen, dass die Reaktionszeit bei einem gewöhnlichen Autofahrer nicht länger ist als eine Sekunde. Berechne den Reaktionsweg, der sich bei einer Geschwindigkeit von (1) 30 km/h,   (2) 50 km/h,   (3) 100 km/h aus einer Reaktionszeit von einer Sekunde ergibt. b) Ermittle eine Formel, mit Hilfe derer man den Reaktionsweg aus der Geschwindigkeit berechnen kann. Geh dabei wieder von einer Reaktionszeit von einer Sekunde aus. c) Ermittle eine möglichst einfache Formel, mit Hilfe derer man den Anhalteweg aus der Geschwindigkeit berechnen kann. d) In der Fahrschule lernt man folgende Formeln: Reaktionsweg = Geschwindigkeit durch 10 mal drei Bremsweg = Geschwindigkeit durch 10 mal Geschwindigkeit durch 10 Anhalteweg = Reaktionsweg + Bremsweg Vergleiche die Fahrschulformeln mit deinen bisherigen Ergebnissen.

Experimentieren mit einem Applet zum Anhalteweg

Im folgenden Applet ist der Zusammenhang zwischen Geschwindigkeit und Anhalteweg dargestellt worden. Mit Hilfe der Schieberegler können einerseits die Reaktionzeit, andererseits die Straßenverhältnise variiert werden.

Anleitung Schieberegler etc. [...]

[Hier muss noch ein GeoGebra-Applet eingefügt werden.]

Aufgabe   a) [...] intuitiv am Graphen arbeiten b) Bei welchem Wert für a ist der Anhalteweg bei einer Geschwindigkeit von 60 km/h ungefähr 83 m lang?

Interaktive Übungen

Liebe Gabi, könntest du diesen Teil übernehmen?

Arbeitsblätter und Links

Arbeitsblätter

• Arbeitsblatt aus dem Sinus-Lernnetz

Links

• Ideen zum Thema "Wurfparabel"
• Allgemeines zu Quadratischen Funktionen
• Bremsweg bei Wikipedia

Dieser Lernpfad wurde erstellt von: Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann und Gabi Jauck