Quadratische Funktionen - Bremsbeschleunigung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: == Unterschiedliche Straßenverhältnisse == Bisher waren wir davon ausgegangen, dass die Länge des Bremsweges lediglich von der Geschwindigkeit abhängt. Das ist nat...) |
Version vom 5. Oktober 2008, 18:35 Uhr
Unterschiedliche Straßenverhältnisse
Bisher waren wir davon ausgegangen, dass die Länge des Bremsweges lediglich von der Geschwindigkeit abhängt. Das ist natürlich Unsinn. Bei gleicher Geschwindigkeit hat ein alter LKW auf schneeglatter Fahrbahn selbstverständlich einen ungleich längeren Bremsweg als ein neuer Kleinwagen auf einer trockenen und sauberen Straße. Diese Einflüsse kommen in der sogenannten "Bremsverzögerung" zum Ausdruck. Die Bremsverzögerung gibt an, wie stark ein Fahrzeug abgebremst wird: Eine hohe Bremsverzögerung spricht also für einen kurzen Bremsweg.
In einer Formel für den Bremsweg sollte also nicht nur die Geschwindigkeit, sondern auch die Bremsverzögerung berücksichtigt werden. In lehrbüchern findet man die Formel:
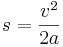(s = Bremsweg in m, v = Geschwindigkeit in m/s und a = Bremsverzögerung in m/s²).
In dem folgenden GeoGebra-Applet kann der Bremsweg variiert werden.
Aufgabe
Wie muss a gewählt werden, damit ... |
