Die Graphen der Funktionen mit f(x) = x-1/n, n ∈ IN
Es sei stets IN0={0,1,2,...} und IN={1,2,3,..}, insbesondere also IN0 =/= IN.
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen negativen Stammbruch der Form 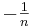 mit
mit 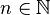 als Exponenten haben. Für diese Art der Exponenten gilt:
als Exponenten haben. Für diese Art der Exponenten gilt: 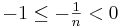 .
.
Vergleich mit Funktionen aus Stufe 3
Aufgabe 1 
Verleiche den neuen Graphen (blau) mit dem, den Du schon aus Stufe 3 dieses Kurses kennst (rot gestrichelt); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern.
- Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
- Definitionsbereich
- Symmetrie
- Monotonie
- größte und kleinste Funktionswerte
- Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen.
HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen
- [Lösung anzeigen][Lösung ausblenden]
- Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-kn-facht.
- Symbolisch
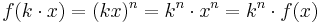 . .
|
|
|
Exponenten, Brüche und Potenzgesetze
Aufgabe 2 
Zeige die Richtigkeit folgender Behauptung:
Ein Funktion
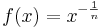
mit einer natürlichen Zahl n hat den Definitonsbereich D = IR+.
|
}
Im vorliegenden Fall betrachten wir negative Stammbrüche als Exponten. Man erinnere sich dabei an die Potenzgesetze, insbesondere an folgenden Zusammenhang:
- Für eine reelle Zahl
 und eine natürliche Zahl und eine natürliche Zahl 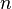 wird definiert: wird definiert:
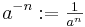 für für 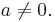
Auf unsere Situation angewandt ergibt sich:
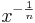 ![= \frac{1}{x^{\frac 1 n}} = \frac{1}{\sqrt[n]{x}}.](/images/math/2/a/8/2a88af2a25634faf61fa1fdd87ae9c0e.png)
|
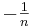 mit
mit 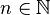 als Exponenten haben. Für diese Art der Exponenten gilt:
als Exponenten haben. Für diese Art der Exponenten gilt: 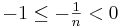 .
.
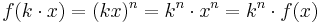 .
.
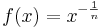
 und eine natürliche Zahl
und eine natürliche Zahl 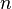 wird definiert:
wird definiert:
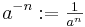 für
für 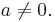
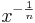
![= \frac{1}{x^{\frac 1 n}} = \frac{1}{\sqrt[n]{x}}.](/images/math/2/a/8/2a88af2a25634faf61fa1fdd87ae9c0e.png)

