Potenzfunktionen - 3. Stufe
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x1/n, n ∈ IN
Es sei stets IN0={0,1,2,...} und IN={1,2,3,..}, insbesondere also IN0 =/= IN.
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen positiven Stammbruch der Form 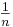 mit
mit 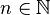 als Exponenten haben. Während in Stufe 1 und 2 dieses Kurses die Exponenten stets ganzzahlig waren, gilt für die Stammbrüche:
als Exponenten haben. Während in Stufe 1 und 2 dieses Kurses die Exponenten stets ganzzahlig waren, gilt für die Stammbrüche: 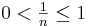 .
.
Vergleich mit Funktionen aus Stufe 2
|
Potenzen und Wurzeln
Eine Funktion  mit der Gleichung
mit der Gleichung ![f(x)=\sqrt[n]{x}](/images/math/8/4/5/845e92e8d6fb632e22343997822d31e4.png) mit
mit 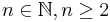 heißt Wurzelfunktion.
heißt Wurzelfunktion.
Potenzfunktionen der Bauart 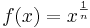 und Wurzelfunktionen
und Wurzelfunktionen ![g(x)=\sqrt[n]{x}](/images/math/f/5/c/f5c0dce3d90d2f6d2d7c95d0201371cf.png) hängen eng zusammen, denn es gilt:
hängen eng zusammen, denn es gilt:
Darin ist die n-te Wurzel über folgenden Zusammenhang festgelegt:
Im Falle 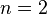 nennt man die Wurzel "Quadratwurzel" und man schreibt:
nennt man die Wurzel "Quadratwurzel" und man schreibt:
Im Falle 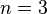 nennt man die Wurzel "Kubikwurzel", i. Z.:
nennt man die Wurzel "Kubikwurzel", i. Z.: 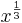 bzw.
bzw. ![\sqrt[3]{x}](/images/math/a/1/0/a10c7f2aa138b1565920d17c22062a35.png) .
.
Beispiel: Quadratwurzel
Eine positive Zahl 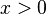 hat zwei Quadratwurzeln, eine positive und eine negative. So ist etwa
hat zwei Quadratwurzeln, eine positive und eine negative. So ist etwa
-
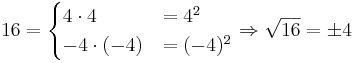 .
.
In manchen Fällen (etwa wenn es um die Bestimmung von Längen oder Flächeninhalten geht) ist nur die postive Lösung sinnvoll.
Beispielsweise ergibt sich die Länge 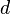 der Diagonale in einem Quadrat der Seitenlänge
der Diagonale in einem Quadrat der Seitenlänge 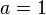 über den Satz des Pythagoras zu:
über den Satz des Pythagoras zu:
Die mathematisch richtige Lösung 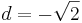 ist in dieser Situation nicht sinnvoll und kann vernachlässigt werden.
ist in dieser Situation nicht sinnvoll und kann vernachlässigt werden.
Beispiel: Kubikwurzel
-
![\sqrt[3]{27}=\sqrt[3]{3\cdot 3 \cdot 3} = \sqrt[3]{3^3} = \sqrt[3]{3}^3 = 3](/images/math/8/2/c/82cd472932df81e17bdcd6ee2c6016b0.png) , aber auch
, aber auch
Definitionsbereich der Wurzelfunktionen
Einschränkung auf IR+
Offenbar ergibt die Wurzelfunktion ![f(x)=\sqrt[n]{x}](/images/math/8/4/5/845e92e8d6fb632e22343997822d31e4.png) zumindest bei ungeradem n sowohl für positive als auch negative x Lösungen, wie folgendes Beispiel zeigt:
zumindest bei ungeradem n sowohl für positive als auch negative x Lösungen, wie folgendes Beispiel zeigt:
Allerdings kann die Definition der Wurzelfunktion auf ganz IR auch zu Wiedersprüchen führen. An einem Beispiel wird die Problematik klar:
Um solche Fälle von Nicht-Eindeutigkeiten oder langen Fallunterscheidungen zu umgehen, schränkt man den Definitionsbereich ID der Wurzelfunktionen i.d.R. grundsätzlich auf die positiven reelle Zahlen ein, also:
![f(x) = \sqrt[n]{x}](/images/math/8/4/5/845e92e8d6fb632e22343997822d31e4.png) mit
mit 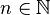 und
und 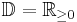
Wurzelfunktion auf ganz IR
Will man eine Wurzelfunktion g dennoch auf ganz IR definieren (d.h. ID = IR), dann muss man sie - nach obiger Vorüberlegung - aus zwei einzelnen Wurzelfunktionen zusammensetzen. Man definiere etwa g derart, dass
![g(x):=\begin{cases}\sqrt[n]{x}, &x\geq 0 \\ -\sqrt[n]{-x}, &x<0\end{cases}](/images/math/a/3/a/a3ab5cc5c79181de2e4fb2b10a3c1493.png) .
.
Dann gilt: IDg = IR.
kurz nachgedacht
- asd asd
- asd asd asd
- aasdd
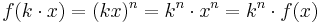 .
.
![x^{\frac{1}{n}}:=\sqrt[n]{x}](/images/math/4/9/9/4999dd3cabd40b13e2c72e4dd52f4963.png)
![\sqrt[n]{x} :\Leftrightarrow \left(\sqrt[n]{x}\right)^n = x](/images/math/a/1/0/a1011f18347a9ec8e5361e70a5d11b8e.png)
![x^{\frac{1}{2}} = \sqrt[2]{x} =: \sqrt{x}](/images/math/0/a/c/0ac01087183dbfa345a1f18b06682aeb.png)
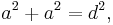
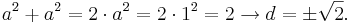
![\sqrt[3]{-27}=\sqrt[3]{-3\cdot -3 \cdot -3} = \sqrt[3]{-3^3} = \sqrt[3]{-3}^3 = -3,](/images/math/6/2/7/627b4363ca82650f81fbfc0aabaeedb9.png)
![\sqrt[3]{ 27}=\sqrt[3]{3\cdot 3 \cdot 3} = \sqrt[3]{3^3} = \sqrt[3]{3}^3 = 3.](/images/math/6/c/c/6cc6c328ea65f968fd01a636602ec89d.png)
![-2 = \sqrt[3]{-8} = (-8)^{\frac{1}{3}} = (-8)^{\frac{2}{6}} = \left( (-8)^2 \right)^{\frac{1}{6}} = \left( (8)^2 \right)^{\frac{1}{6}} = (8)^{\frac{2}{6}} = (8)^{\frac{1}{3}} = \sqrt[3]{8} = 2.](/images/math/6/1/6/6165c6f8f1d60ceda3379d42bb03efe8.png)

