Diskret - kontinuierlich
|
Über diesen Lernpfad
Schüler/innen sollen sich mit der Beschreibung von dynamischen Vorgängen beschäftigen und den Unterschied zwischen diskreten Vorgängen (Beschreibung über Differenzengleichungen) und kontinuierlichen Vorgängen (Beschreibung über Differentialgleichungen) kennen lernen. Kompetenzen
|
Inhaltsverzeichnis |
Rekursive Beschreibung von Veränderungen
Numerische Näherung - Heronverfahren
Radioaktiver Zerfall
Räuber-Beute-Modell
Differenzengleichung
Begriffsbildung
Eine Differenzengleichung ist eine Möglichkeit, dynamische Systeme abzubilden. Dabei wird eine Folge von diskreten (einzeln betrachtbaren, "abzählbaren") Ereignissen rekursiv definiert. Jedes Folgenglied ist daher eine Funktion der vorhergehenden Folgenglieder.
Form: 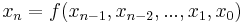
für natürliche Zahlen n.
Die Veränderung wird durch den Differenzenquotienten angegeben:
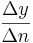
mit 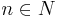
Dabei entspricht:
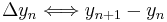 und damit beispielsweise
und damit beispielsweise 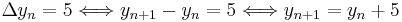
Links:
- http://statmath.wu-wien.ac.at/~leydold/MOK/HTML/node187.html, Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997
Marktgleichgewicht - Cobweb-DIagramm
Cobweb / Spinnwebdiagramme stellen eine gute Möglichkeit dar, Rekursionen darzustellen.
Links:
- Spinnwebdiagramme - Lineare Differenzengleichungen 1. Ordnung mit GeoGebra: http://www.geogebra.org/de/wiki/index.php/Lineare_Differenzengleichung_1._Ordnung
Von der diskreten zur kontinuierlichen Veränderung
Exponentielles Wachstum - Lebensmittelkontrolle
Radioaktiver Zerfall - analytische Herleitung
Die Gleichung 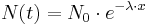 ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften ist es nun mit Hilfe der Integralrechung möglich, ausgehen vom Ansatz
ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften ist es nun mit Hilfe der Integralrechung möglich, ausgehen vom Ansatz 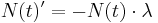 obige Relationen per Differentiagleichung analytisch herzuleiten.
Unter Rad_zerfall_analytisch.pdf ist diese Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und sich dann auf die Anwendung beim radioaktiven Zerfall bezogen.
obige Relationen per Differentiagleichung analytisch herzuleiten.
Unter Rad_zerfall_analytisch.pdf ist diese Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und sich dann auf die Anwendung beim radioaktiven Zerfall bezogen.
Zusätzlich sind drei Standardaufgaben angegeben, um die Verwendung der Gleichung zu wiederholen.
Beispiele zum radioaktiven Zerfall
Halbwertszeit
Der Zeitraum, in dem eine (meist exponentiell) abfallende Größe auf die Hälfte ihres Anfangswertes abgesunken ist. Die physikalische Halbwertszeit ist die für jedes Isotop eines radioaktiven Elementes charakteristische Zeitdauer, in der von einer ursprünglichen vorhandenen Anzahl radioaktiver Kerne bzw. instabilen Elementarteilchen die Hälfte zerfallen ist (entnommen aus Brockhaus in 5 Bänden, zweiter Band).
|
Jod-131 hat eine Halbwertszeit von 8 Tagen. Berechne den Parameter λ (Basiszeiteinheit 1 Tag und 1 Jahr) in der Zerfallsgleichung auf 6 gültige Nachkommastellen! |
|
Von Kobalt-60 ist nach 3,88 Jahren 40% des Ausgangsmaterials zerfallen. Wie groß ist die Halbwertszeit dieses Isotops? |
|
Von 24000 Cäsium-137-Kernen sind nach einer bestimmten Zeit |
Aufgaben im pdf-Format
Die Angaben zu den Aufgaben findet man unter Bsp_rad_zerfall.pdf (43 kb).
Lösungen im pdf-Format
Die Lösungen zu diesen Aufgaben findet man unter Lösungen zu Bsp_rad_zerfall.pdf (59 kb).
Abbau von Giftstoffen
Logistisches Wachstum - beschränktes Wachstum
Ein-Lebewesen-Modell nach Verhulst
Differentialgleichungen
Begriffsbildung
Als (gewöhnliche) Differenzialgleichung (DGLG) wird eine Gleichung bezeichnet, die neben einer Unbekannten 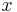 auch deren Ableitung(en)
auch deren Ableitung(en) 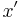 (
(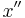 , ...) enthält. Gelöst wird eine DGLG mittels Integralrechnung.
, ...) enthält. Gelöst wird eine DGLG mittels Integralrechnung.
Die Lösung einer DGLG ist nicht wie bei einer herkömmlichen Gleichung eine Zahl, sondern eine Funktion, genauer eine Funktionenschar, die aus unendlich vielen Funktionen besteht. Da beim unbestimmten Integrieren immer eine Integrationskonstante auftritt, muss eine Zusatzinformation (Anfangsbedingung) gegeben sein, um die Konstante zu bestimmen.
Erst durch die Anfangsbedingung, die einem Punkt auf dem Graphen der Lösungsfunktion entspricht, kann die Lösungsfunktion exakt bestimmt werden. Die Lösung ist nun eine spezielle Funktion!
DGLG können in allen Bereichen des Lebens angetroffen werden, besonders in den Naturwissenschaften oder der Wirtschaft und dem Sport. In allen Zusammenhängen, bei denenen es um Veränderungen geht, kommen DGLG zur Anwendung.
Eine Übersicht über die Klassifikation von DGLG findet man unter http://www.math.tu-berlin.de/geometrie/Lehre/SS05/GDglmA/skriptKlassif.pdf
Links:
- http://statmath.wu-wien.ac.at/~leydold/MOK/HTML/node175.html, Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997
Lösung einfacher Differentialgleichungen
Ausblick
Visualisierung über Richtungsfelder
Näherungsverfahren
© 2009, Projekt "Medienvielfalt im Mathematikunterricht"
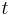 21771 Kerne zerfallen. Die Halbwertszeit des Isotops beträgt 2,1 Jahre. Berechne
21771 Kerne zerfallen. Die Halbwertszeit des Isotops beträgt 2,1 Jahre. Berechne 
