Potenzfunktionen - 3. Stufe
Es sei stets 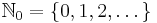 und
und 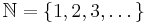 , insbesondere also
, insbesondere also 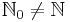 .
.
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen (positiven) Stammbruch der Form 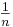 mit
mit 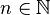 als Exponenten haben. Während in Stufe 1 und 2 dieses Kurses die Exponenten stets ganzzahlig waren, gilt für die Stammbrüche:
als Exponenten haben. Während in Stufe 1 und 2 dieses Kurses die Exponenten stets ganzzahlig waren, gilt für die Stammbrüche: 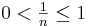 .
.
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x1/n, n ∈ IN
Funktionsgraph kennenlernen
|
Vergleich mit Funktionen aus Stufe 2
|
Bezeichungen: Potenzen und Wurzeln
Wir betrachten hier Potenzfunktionen mit 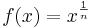 ,
, 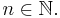
Wegen ![x^{\frac{1}{n}}:=\sqrt[n]{x}](/images/math/4/9/9/4999dd3cabd40b13e2c72e4dd52f4963.png) nennt man diese Funktionen auch Wurzelfunktionen. Ihr Definitionsbereich ID ist - wie die Aufgaben 1 und 2 gezeigt haben - nicht negativ (Nähere Erläuterungen hierzu: siehe unten) , also ID = IR+0
nennt man diese Funktionen auch Wurzelfunktionen. Ihr Definitionsbereich ID ist - wie die Aufgaben 1 und 2 gezeigt haben - nicht negativ (Nähere Erläuterungen hierzu: siehe unten) , also ID = IR+0
Im Falle 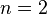 nennt man die Wurzel "Quadratwurzel" und man schreibt:
nennt man die Wurzel "Quadratwurzel" und man schreibt:
Im Falle 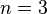 nennt man die Wurzel "Kubikwurzel", i. Z.:
nennt man die Wurzel "Kubikwurzel", i. Z.: 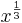 bzw.
bzw. ![\sqrt[3]{x}](/images/math/a/1/0/a10c7f2aa138b1565920d17c22062a35.png) .
.
Beispiel: Quadratwurzeln
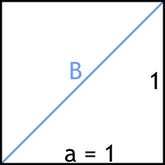
Beispielsweise ergibt sich die Länge 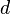 der Diagonale in einem Quadrat der Seitenlänge
der Diagonale in einem Quadrat der Seitenlänge 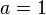 über den Satz des Pythagoras (
über den Satz des Pythagoras (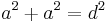 ) zu:
) zu:
Die Lösung ist 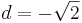 ergibt hier keinen Sinn, da wir nur Längen in der realen Welt betrachten.
ergibt hier keinen Sinn, da wir nur Längen in der realen Welt betrachten.
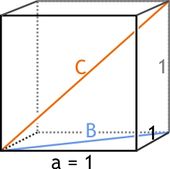
Auch die Länge der Raumdiagonale 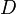 im Einheitswürfel (das ist ein Würfel mit der Kantenlänge s=1) ergibt sich über eine analoge Rechnung aus dem Satz des Satz des Pythagoras (hier:
im Einheitswürfel (das ist ein Würfel mit der Kantenlänge s=1) ergibt sich über eine analoge Rechnung aus dem Satz des Satz des Pythagoras (hier: 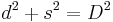 ) zu:
) zu:
Die Lösung ist also 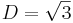 angeben.
angeben.
Beispiel: Kubikwurzel
Das Volumen 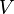 eines Würfels (lat.: "cubus") der Kantenlänge
eines Würfels (lat.: "cubus") der Kantenlänge 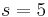 ergibt sich über:
ergibt sich über:
Umgekehrt erhält man die Kantenlänge eines Würfels mit Volumen 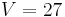 durch ziehen der 3.-Wurzel:
durch ziehen der 3.-Wurzel:
Einfluss von Parametern
|
In nebenstehendem Applet kannst Du die Parameter
|
*Zum Weiterdenken: Definitionsbereich der Wurzelfunktionen
Einschränkung auf IR+0
Gelegentlich findet man in Büchern oder auch im Internet folgende Darstellung: ![\sqrt[3]{-8}= -2,](/images/math/5/b/6/5b6fa0df280fc90fa5e52cf58c8949fc.png)
Wegen
erscheint das richtig zu sein, allerdings kann diese Festlegung zu Widersprüchen führen, wie das folgende Beispiel zeigt:
Um solche Fälle von Nicht-Eindeutigkeiten, aber auch um Fallunterscheidungen bei 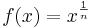 für gerade und ungerade n zu vermeiden, schränkt man den Definitionsbereich ID der Wurzelfunktionen grundsätzlich auf die nicht-negativen reellen Zahlen ein, also:
für gerade und ungerade n zu vermeiden, schränkt man den Definitionsbereich ID der Wurzelfunktionen grundsätzlich auf die nicht-negativen reellen Zahlen ein, also:
![f(x) = \sqrt[n]{x}](/images/math/8/4/5/845e92e8d6fb632e22343997822d31e4.png) mit
mit 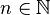 und
und 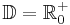
Wurzelfunktion auf ganz IR
Will man eine Wurzelfunktion g dennoch auf ganz IR definieren (d.h. ID = IR), dann muss man sie - nach obiger Vorüberlegung - aus zwei einzelnen Wurzelfunktionen zusammensetzen. Man definiere etwa g derart, dass
![g(x):=\begin{cases}\sqrt[n]{x}, &x\geq 0 \\ -\sqrt[n]{-x}, &x<0\end{cases}](/images/math/a/3/a/a3ab5cc5c79181de2e4fb2b10a3c1493.png) .
.
Dann gilt: IDg = IR.
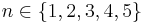 .
.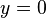 wird für
wird für  angenommen; von da aus steigen die blauen Graphen steng monoton an. Symmetrien (Achsen- bzw. Punktsymmetrie) findet man nur für die rot gestrichelten, nicht aber für die blauen Graphen.
angenommen; von da aus steigen die blauen Graphen steng monoton an. Symmetrien (Achsen- bzw. Punktsymmetrie) findet man nur für die rot gestrichelten, nicht aber für die blauen Graphen.
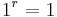 für alle
für alle 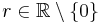 .
.
![x^{\frac{1}{2}} = \sqrt[2]{x} =: \sqrt{x}](/images/math/0/a/c/0ac01087183dbfa345a1f18b06682aeb.png)
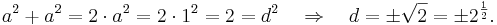
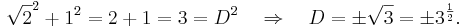
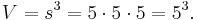
![\sqrt[3]{27}=\sqrt[3]{3\cdot 3 \cdot 3} = \sqrt[3]{3^3} = \sqrt[3]{3}^3 = 3.](/images/math/6/c/c/6cc6c328ea65f968fd01a636602ec89d.png)
 und
und  mit den Schiebereglern verändern.
mit den Schiebereglern verändern.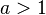 eine Streckung des Graphen in y-Richtung, für
eine Streckung des Graphen in y-Richtung, für 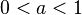 eine Stauchung in y-Richtung; für
eine Stauchung in y-Richtung; für 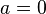 erhält man eine konstante Funktion mit
erhält man eine konstante Funktion mit 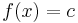 . Wird
. Wird  zu einer monoton fallenden Funktion.
zu einer monoton fallenden Funktion.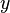 der Wert
der Wert 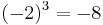
![-2 = \sqrt[3]{-8} = (-8)^{\frac{1}{3}} = (-8)^{\frac{2}{6}} = \left( (-8)^2 \right)^{\frac{1}{6}} = \left( (8)^2 \right)^{\frac{1}{6}} = (8)^{\frac{2}{6}} = (8)^{\frac{1}{3}} = \sqrt[3]{8} = 2.](/images/math/6/1/6/6165c6f8f1d60ceda3379d42bb03efe8.png)

