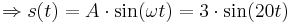Lösung zu Aufgabe 4
Aus Medienvielfalt-Wiki
< Trigonometrische Funktionen | Bestimmung der Funktionsgleichung aus dem Graphen
Version vom 6. Juli 2009, 12:23 Uhr von Silvia Joachim (Diskussion | Beiträge)
Lösung zu Aufgabe 4
1. Die Schwingungsdauer kann sehr genau bestimmt werden, indem man zunächst zwei Nullstellen wählt, die sehr genau abgelesen werden können.
- Nullstellen:
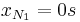 und
und 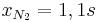
- Da in 1,1 Sekunden 3,5 Schwingungen stattfinden, erhält man als Schwingungsdauer:
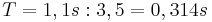
- Frequenz:
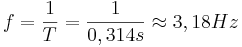
2. 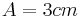 und
und 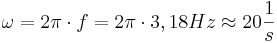 oder
oder 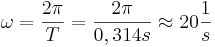
Nullstellen der Sinusfunktion: 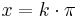 mit
mit  oder
oder 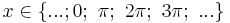
Nullstellen: 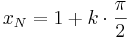 mit
mit  oder
oder 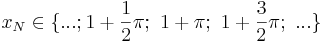
Hochpunkte: 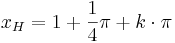 mit
mit  oder
oder 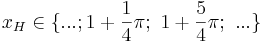
Tiefpunkte: 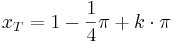 mit
mit  oder
oder 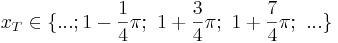
streng monoton fallend: ![...;\ [1+\frac{1}{4}\pi;\ 1+\frac{3}{4}\pi];\ [1+\frac{5}{4}\pi;\ 1+\frac{7}{4}\pi];\ ...](/images/math/3/8/c/38cede13d42a4986bf3d2217920545d4.png)
streng monoton steigend: ![...;\ [1-\frac{1}{4}\pi;\ 1+\frac{1}{4}\pi];\ [1+\frac{3}{4}\pi;\ 1+\frac{5}{4}\pi];\ ...](/images/math/9/d/1/9d17ad4a42698cc2f951c8cadb0f83ad.png)