Quadratische Funktionen - Stationenbetrieb

Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Stationenbetrieb - Allgemeine quadratische Funktion - Übungen 3

Abschließend zu dem Thema "Bremsweg" sollst du nun die folgenden Stationen bearbeiten. Dazu benötigst du Wissen, wie man den Bremsweg, den Reaktionsweg und den gesamten Anhalteweg berechnet. Diese Informationen werden dir übersichtshalber zur Verfügung gestellt. Dabei handelt es sich auch um Informationen, die wir bis dahin noch nicht durchgenommen haben:

                                             Erforderliche Information zur Bearbeitung der Stationen 

                                                                   Formeln zum Anhalteweg

Erläuterung: Der Reaktionsweg ist der Weg, den man während der sogenannten Schreckse-kunde (Reaktionszeit) zurücklegt.

tr	Reaktionszeit in sec
v	Ausgangsgeschwindigkeit in m/sec
ab	Bremsbeschleunigung in m/sec²
sa	Anhalteweg
sr	Reaktionsweg
sb	Bremsweg

s_r = t_r x v
s_b = [1:(2a_b)] x v²

 Anhalteweg  = Reaktionsweg + Bremsweg

 sa = sr + sb

 sa = tr x v + $\frac{1}{2  a(b)}$ x v² , wobei a(b) für die Bremsbeschleunigung steht.

Beachte : Rechne nicht in km/h, sondern wandle in m/sec um.


Zur Reaktionszeit
Die Reaktionszeit t_r ist abhängig von der Situation (Muss ich bremsen? Kann ich noch ausweichen? . . .) und dem Fahrer (Fahrstil, Gesundheit, Müdigkeit, Alkohol, . . .).

Normalfall	1,0 sec
abgelenkter Autofaher	2,0 sec
alkoholisierter Fahrer	2,5 sec
Rennfahrer	0,7 sec

Für PKW bei Straßenzustand
Glatteis	1,0 – 1,5 m/sec²
Neuschnee (mit Sommerreifen)	2,0 – 2,5 m/sec²
Neuschnee (mit Winterreifen)	2,5 – 3,0 m/sec²
Asphalt trocken	6,5 – 7,5 m/sec²
Asphalt nass	5,0 – 6,5 m/sec²
Beton trocken	6,5 – 7,5 m/sec²
Beton nass	4,0 – 5,5 m/sec²
Kopfsteinpflaster trocken	5,5 – 6,5 m/sec²
Kopfsteinpflaster nass	4,5 – 5,5 m/sec²
Andere Fahrzeuge bei trockenem Asphalt
Fahrrad	2,5 – 3,5 m/sec²
Motorrad	3,5 – 4,5 m/sec²
Pkw mit ABV	8,5 – 9,0 m/sec²

Schreibe alle Lösungsberechnungen der Aufgaben in dein Heft! Vergleiche danach deine Lösung mit der angegebenen "Musterlösung".

Station 1 

Die Unfallstatistiken zeigen: Nicht angepasste Geschwindigkeit und ungenügender Sicher-heitsabstand sind zunehmend Hauptunfallursachen im Straßenverkehr.

1) In welchem Bereich liegt der Anhalteweg eines "normalen" Autofahrers?

Geschwindigkeit in	Anhalteweg auf trockenem Asphalt	Anhalteweg auf nassem Asphalt
Km/h
50 Km/h
130 Km/h

2) In der Fahrschule wird behauptet:
Der Anhalteweg eines alkoholisierten Fahrers ist im Stadtverkehr bei Tempo 50 mehr als 20 m länger als bei einem nüchternen, „normalen“ Fahrer. Gutes Fahrvermögen (z.B. von Rennfahrern) hat nur wenig Auswirkung auf die Länge des Anhalteweges. Überprüfe die Behauptungen!

 Station 2 

Denk dir diese Situation:
Ein Auto fährt mit 30 km/h auf einer Wohngebietsstraße. Ein anderer Autofahrer „hat es eilig“ und überholt mit 50 km/h. In dem Moment, in dem beide Autos gleichauf sind, springt ein Kind in einiger Entfernung auf die Fahrbahn. Zum Glück ist der Asphalt trocken, beide Autos sind topfit in Schuss und beide Autofahrer sind hellwach, so dass sie eine Sekunde später eine Vollbremsung machen. Das 30 km/h – Auto kommt noch eben rechtzeitig zum Stehen, haarscharf vor dem Kind.

1. Wie viele Meter vor den beiden Autos springt das Kind auf die Straße?
2. Mit welcher Geschwindigkeit würde das 50 km/h – Auto auf das Kind prallen? (Hinweis: Berechne zunächst den Reaktionsweg.)

 Station 3 

Nicht angepasste Geschwindigkeit und ungenügender Sicherheitsabstand, aber auch Ablen-kungen durch Telefonieren, Rauchen, Essen, usw. sind zunehmend Hauptunfallursachen im Straßenverkehr.

1.
a) Wie verändert sich der Anhalteweg, wenn sich die Geschwindigkeit erhöht ? (Man sagt: Wie verändert sich der Anhalteweg in Abhängigkeit von v ?)
b) Begründe anhand der Formel s_v = t_r x v + 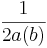$\frac{1}{2 a(b)}$ x v² (wobei a(b) für die Bremsbeschleunigung steht), warum es sich um den Teil einer Parabel handelt.
2.
a) Wie verändert sich der Anhalteweg in Abhängigkeit von der Reaktionszeit?
b) Begründe anhand der Formel s_t = t_r x v + 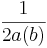$\frac{1}{2 a(b)}$ x v², warum es sich um eine Gerade handelt.

 Station 4 

So funktioniert die "Blechbremse" an der Felswand

Bei Bergfahrten kann es schon einmal passieren, dass die Bremse ausfällt. Dann bleibt nur noch die Blechbremse um anhalten zu können. Berühren Sie mit der rechten Fahrzeugseite so sanft wie möglich die Felswand. Kalkulieren Sie dabei ein, dass Ihnen das Lenkrad aus der Hand gerissen wird. Halten Sie daher die Dau-men außen. Drehen Sie nach dem ersten Aufprall das Lenkrad etwas stärker bergwärts und schrammen Sie in dieser Stellung den Berg entlang.

v in km/h	10	20	30	40	50	60	80
v in m/sec
sb in m	0,6	2,3	4,6	8,9	15,3	22,7
ab in m/sec²

1. Ermittle die durchschnittliche Bremsverzögerung b.
2. Bestimme den Bremsweg für 80 km/h.

 Station 5 

Ein Unfallgutachter bekommt den Auftrag an Hand der Bremsspuren bei einem Unfall, bei dem ein Kind angefahren wurde, die Geschwindigkeit des Autos zu ermitteln. Der Unfall ereignete sich in einer geschlossenen Ortschaft und der Autofahrer behauptete, dass er die vorgeschriebene Höchstgeschwindigkeit von 50 km/h nicht überschritten habe. Aus den Unterlagen der Polizei geht hervor, dass die Bremsspur eine Länge von 19,3 m hat. Der Asphalt war am Unfalltag trocken und griffig.

1. Zu welchem Ergebnis wird der Gutachter unter diesen Voraussetzungen kommen?

Aus den Aussagen des Autofahrers und weiterer Zeugen geht hervor, dass er ca. 30 m Abstand von der Unfallstelle hatte, als das Kind auf die Straße gesprungen ist. Etwa 5 m vor dem Ende der Bremsspur wurde das Kind vom Auto erfasst und zur Seite geschleudert.

2. Was lässt sich daraus über die Reaktionszeit des Autofahrers erschließen?

Der Gutachter soll auch Auskunft darüber geben, bei welcher Geschwindigkeit der Fahrer das Auto noch rechtzeitig hätte anhalten können.

3. Führe die notwendigen Berechnungen für eine Reaktionszeit von einer bzw. zwei Se-kunden durch.

4. Wie würdest du den Fall als Jurist beurteilen?

Als nächstes lernst du die allgemeine quadratische Funktion kennen.   Hier geht es weiter.

<u>Unterstrichener Text</u> Klein