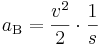Quadratische Funktionen Station1
Einstieg
Ist bei doppelter Geschwindigkeit auch der Bremsweg doppelt so lang? Was meinst du?
Diese Frage wurde im Fernsehen bei Kopfball.de untersucht. In dem Video aus der Sendung findest du eine Antwort!! Wenn du dir das Video in der Schule anschaust, benutze bitte Kopfhörer und stelle die Lautsprecher leiser.
- Trage ins Heft ein
Bei der weiteren Bearbeitung dieser Station musst du dir unter 5 Quadratische Funktionen, mit der Überschrift Einführung - Bremsweg folgendes unbedingt ins Merkheft aufschreiben:
- Welche Formel wird in der Fahrschule herkömmlicherweise zur Berechnung des Bremsweges verwendet?
- Erläutere den Begriff "Bremsbeschleunigung".
- Welche (exaktere) Formel berücksichtigt auch die Bremsbeschleunigung?
Tabelle, Graph und Formel
Die Polizei hat Messungen durchgeführt, um den Zusammenhang zwischen der Geschwindigkeit eines Autos und seinem Bremsweg zu erkunden. Klar ist: Je schneller eine Auto fährt, desto länger ist sein Bremsweg. Aber ist das wirklich so einfach...?
Du kannst den Zusammenhang selbst untersuchen. Hier sind die Daten, die die Polizei gesammelt hat:
Geschwindigkeit v (in km/h) 10 20 30 40 50 80 100 120 Bremsweg s (in m) 1 4 9 16 25 64 100 144
|
Lösung: Starte GeoGebra mit dem folgenden Knopf, um die fertige Zeichnung zu sehen:
|
- z.B.
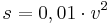 oder
oder 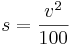 (dabei ist s der Bremsweg in Metern und v die Geschwindigkeit in km/h)
(dabei ist s der Bremsweg in Metern und v die Geschwindigkeit in km/h)
- Fahrschulformel:
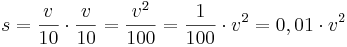 . Die Formeln stimmen also überein.
. Die Formeln stimmen also überein.
- Bemerkung: Die Formeln stimmen nur für gewöhnliche, nicht für "Gefahren"-bremsungen.
| In einem ruhigen Wohnviertel in Niederbremsbach hat Herr Mütze fast ein kleines Mädchen angefahren, das ihrem auf die Straße rollenden Ball hinterher lief. Obwohl das Mädchen mit dem Schrecken davonkam, soll nun geklärt werden, ob sich Herr Mütze an die Geschwindigkeitsbegrenzung von 50 km/h gehalten hatte. Dem Unfallprotokoll ist zu entnehmen, dass Herr Mütze eine Bremsspur von 30,25 Metern erzeugt hat. |
|
- Nach obiger Tabelle hätte Herr Mütze, falls er sich an die Geschwindigkeitsbegrenzung gehalten hätte, allenfalls einen Bremsweg von 25 m haben dürfen.
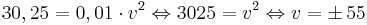
- Nach der Formel aus Aufgabe 1 war Herr Mütze 55 km/h schnell.
- Bemerkung: Tatsächlich ist der Bremsweg bei einer "Gefahrenbremsung" nur etwa halb so lang wie in der obigen Tabelle angegeben. Geht man von einer "Gefahrenbremsung" aus, so käme man auf eine Geschwindigkeit von fast 78 km/h!
Unterschiedliche Straßenverhältnisse
Bisher waren wir davon ausgegangen, dass die Länge des Bremsweges lediglich von der Geschwindigkeit abhängt. Das ist in der Realität natürlich nicht der Fall. Bei gleicher Geschwindigkeit hat ein alter LKW auf schneeglatter Fahrbahn selbstverständlich einen ungleich längeren Bremsweg als ein neuer Kleinwagen auf einer trockenen und sauberen Straße. Diese Einflüsse kommen in der sogenannten Bremsbeschleunigung zum Ausdruck.
Die Bremsbeschleunigung gibt an, wie stark ein Fahrzeug abgebremst wird: Eine hohe Bremsbeschleunigung spricht also für einen kurzen Bremsweg.
In einer Formel für den Bremsweg sollte also nicht nur die Geschwindigkeit, sondern auch die Bremsbeschleunigung berücksichtigt werden. In Lehrbüchern findet man die Formel:
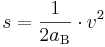 (s = Bremsweg in m, v = Geschwindigkeit in m/s und aB = Bremsbeschleunigung in m/s²).
(s = Bremsweg in m, v = Geschwindigkeit in m/s und aB = Bremsbeschleunigung in m/s²).
In dem folgenden GeoGebra-Applet kann der Bremsweg mit Hilfe der beiden Schieberegler oben links variiert werden.
Hinweis: Der Einfachheit halber wurde der obige Zusammenhang so verändert, dass die Geschwindigkeit in km/h angegeben wird.
|
Wie muss aB gewählt werden, damit ...
Nutze zur Lösung der Aufgabe das obere Applet. Um die Werte exakt einstellen zu können, klicke den Schieberegler an und verwende dann die Pfeiltasten.
|
In der Realität hängt der Wert der Bremsbeschleunigung aB von verschiedenen Faktoren ab. Im folgenden Video wird der Einfluss der Temperatur der Bremsen auf den Bremsweg untersucht. Der Pkw wird immer von einer Geschwindigkeit von 100 km/h bis zum Stillstand abgebremst und dabei der Bremsweg ermittelt.
|
|