Zurück zu 6. Allgemeine quadratische Funktion
|
Wir betrachten nun den Einfluss von 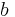 in in 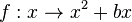 . .
-
-
Aufgabe B2 
- Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen!
|
|
| Die Funktionen, die wir in diesem Kapitel betrachtet haben, sind auch quadratische Funktionen. Sie haben den Funktionsterm ax2 + bx.
Wir lassen den Wert für a gleich und verändern nur den Wert für b.
Aufgabe B3 
- Untersuche an dem Applet rechts den Einfluss von b auf den Verlauf des Graphen.
- Was bleibt gleich?
- Was ändert sich?
|
Aufgabe B4 
- Gibt es einen Zusammenhang zwischen dem blauen und grünen Graphen? Experimentiere erneut mit dem Applet und bestätige deine Vermutung.
- Setzt den Satz fort: "Die Graphen liegen spiegelbildlich bezüglich der y-Achse für ...
|
|
|
|
Aufgabe B1: [Lösung anzeigen][Lösung ausblenden]
- Man erhält den Graph der Funktion
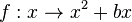
- aus dem Graph der Quadratfunktion
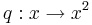 durch Verschiebung sowohl in x- wie auch in y-Richtung durch Verschiebung sowohl in x- wie auch in y-Richtung
- Genauer:
- Ist b > 0, so wird die Normalparabel schräg nach links unten verschoben.
- Ist b < 0, so wird die Normalparabel schräg nach recht unten verschoben.
- Je größer der Betrag von b ist, desto mehr wird in y-Richtung verschoben
- Der Graph zu -b ist spiegelsymmetrisch bezüglich der y-Achse zum Graph von b.
- Die Scheitel aller Graphen zu
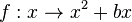 liegen auf der dem Graphen der Funktion liegen auf der dem Graphen der Funktion 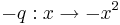
Aufgabe B2: [Lösung anzeigen][Lösung ausblenden]
- Zum Graph der Quadratfunktion
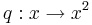 , der Normalparabel, wird noch die Gerade y = bx addiert. Daher kommt für positives b im III.Quadrant ein negativer und im I. Quadrant ein positiver Anteil, für negatives b im II.Quadrant ein positiver und im IV. Quadrant ein negativer Anteil dazu. Dies bewirkt eine Verschiebung des Scheitels. Ansonsten hat der Graph weiterhin das Aussehen einer Normalparabel. , der Normalparabel, wird noch die Gerade y = bx addiert. Daher kommt für positives b im III.Quadrant ein negativer und im I. Quadrant ein positiver Anteil, für negatives b im II.Quadrant ein positiver und im IV. Quadrant ein negativer Anteil dazu. Dies bewirkt eine Verschiebung des Scheitels. Ansonsten hat der Graph weiterhin das Aussehen einer Normalparabel.
Aufgabe B3: [Lösung anzeigen][Lösung ausblenden]
- Die Weite der Parabel bleibt gleich.
- Der Scheitel wird verschoben.
Aufgabe B4: [Lösung anzeigen][Lösung ausblenden]
- Der blaue und der grüne Graph liegen symmetrisch zur y-Achse.
- Die Graphen liegen spiegelbildlich bezüglich der y-Achse für b = 2 und b = -2.
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe B1 ein Hefteintrag "versteckt" ist!
Zurück zu 6. Allgemeine quadratische Funktion
|
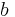 in
in 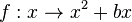 .
.
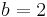 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 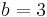 und
und 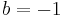 sowie
sowie 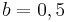 auf den Graphen auswirken und überprüfe deine Vermutung.
auf den Graphen auswirken und überprüfe deine Vermutung. 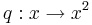 durch Verschiebung sowohl in x- wie auch in y-Richtung
durch Verschiebung sowohl in x- wie auch in y-Richtung