Logistisches Wachstum - beschränktes Wachstum: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „ Zurück zum Lernpfad“)
 
 
(2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
Als <b>logistische Gleichung</b> wird eine Differenzengleichung der Form <math>x_{n+1}=r\cdot x_{n}\cdot(1-x_{n})</math> bezeichnet. Sie wird verwendet, um ein Wachstum mit Schranke (eine maximale Populationszahl) zu modellieren. Die <math>\,x_{i}</math> liegen im Intervall zwischen <math>\,0</math> und <math>\,1</math> und beschreiben die Größe einer Population prozentuell. In der Konstanten <math>r</math> sind Parameter wie Wachstumsrate, Sterblichkeit und Ähnliches zusammengefasst. Die zugehörige Differentialgleichung (DGLG) sieht folgendermaßen aus: <br><br> <math>f'(t)=r\cdot f(t)\cdot(1-f(t))</math>
  
 +
Diese DGLG kann analytisch gelöst werden, was unterhalb für Dich durchgerechnet ist. Zur besseren Lesbarkeit wird statt <math>\,f(t) </math> einfach <math>\,f</math>geschrieben.  <br><br>
 +
<math>
 +
\frac{df}{dt}=r\cdot f\cdot (1-f)
 +
</math>
  
−
[[Diskret - kontinuierlich|Zurück zum Lernpfad]]
+
<math>
 +
\frac{df}{f\cdot (1-f)}=r \cdot dt
 +
</math>
 +
 
 +
<math>
 +
\int \frac{df}{f\cdot (1-f)}=\int r \cdot dt
 +
</math>
 +
 
 +
<math>
 +
\int \frac{A}{f}+\frac{B}{1-f} \cdot df=\int r \cdot dt
 +
</math>
 +
 
 +
Mittels Partialbruchzerlegung ermittelt man für <math>\,A </math> und <math>\,B </math> jeweils den Wert <math>\,1 </math>.
 +
 
 +
<math>
 +
\int \frac{1}{f}+\frac{1}{1-f} \cdot df=\int r \cdot dt
 +
</math> 
 +
 
 +
<math>
 +
ln f - ln(1-f) = r\cdot t + C
 +
</math>
 +
 
 +
<math>
 +
ln \frac{f}{1-f} = r\cdot t + C
 +
</math>
 +
 
 +
<math>
 +
\frac{f}{1-f} = e^{r\cdot t + C}
 +
</math>
 +
 
 +
<math>
 +
f = e^{r\cdot t + C}(1-f)=e^{r\cdot t + C}-e^{r\cdot t + C}\cdot f
 +
</math>
 +
 
 +
 
 +
<math>
 +
f+e^{r\cdot t + C}\cdot f = e^{r\cdot t + C}
 +
</math>
 +
 
 +
<math>
 +
f\cdot(e^{r\cdot t + C}+1) = e^{r\cdot t + C}
 +
</math>
 +
 
 +
<math>
 +
f = \frac{e^{r\cdot t + C}}{(e^{r\cdot t + C}+1)}=\frac{1}{1+\frac{1}{e^{r\cdot t + C}}}
 +
</math>
 +
 
 +
Die Lösungsfunktion der logistischen DGLG lautet nun:
 +
 
 +
<math>
 +
f(t)=\frac{1}{1+e^{-r\cdot t +C}}
 +
</math>
 +
<br><br>
 +
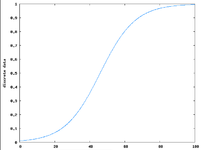
[[:Bild:Logistisches_wachstum.png|<b>Graph der Funktion in besserer Auflösung!</b>]] [[Datei:Logistisches wachstum.png|miniatur|x150px|Graph der logistischen Funktion]] (png-Datei, 5 kB)
 +
<br>
 +
Die Integrationskonstante <math>\,C </math> kann mittels der Anfangsbedingung <math>\,A(0/f_{0})</math> ermittelt werden.
 +
 
 +
<math>
 +
f_{0}=\frac{1}{1+e^{-r\cdot 0 +C}}=\frac{1}{1+e^{C}}
 +
</math>
 +
 
 +
<math>
 +
f_{0}\cdot(1+e^{C})=1
 +
</math>
 +
 
 +
<math>
 +
1+e^{C}=\frac{1}{f_{0}}
 +
</math>
 +
 
 +
<math>
 +
e^{C}=\frac{1}{f_{0}}-1
 +
</math>
 +
 
 +
<math>
 +
C=ln(\frac{1}{f_{0}}-1)
 +
</math>
 +
 
 +
mit <math>\,f_{0}<0</math>, da die maximale Population auf <math>\,1 </math> normiert ist. <br><br>
 +
 
 +
Die komplette Lösung lautet nun:
 +
 
 +
<math>
 +
f(t)=\frac{1}{1+e^{-r\cdot t +ln(\frac{1}{f_{0}}-1)}}
 +
</math>
 +
 
 +
Link:
 +
* [http://de.wikipedia.org/wiki/Logistisches_Wachstum Wikipedia]
 +
 
 +
 
 +
[[Von_der_diskreten_zur_kontinuierlichen_Veränderung#Themengebiete|Zurück zu Von der diskreten zur kontinuierlichen Veränderung]]

Aktuelle Version vom 24. August 2011, 14:27 Uhr

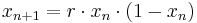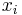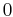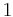Als logistische Gleichung wird eine Differenzengleichung der Form x_{n+1}=r\cdot x_{n}\cdot(1-x_{n}) bezeichnet. Sie wird verwendet, um ein Wachstum mit Schranke (eine maximale Populationszahl) zu modellieren. Die \,x_{i} liegen im Intervall zwischen \,0 und \,1 und beschreiben die Größe einer Population prozentuell. In der Konstanten r sind Parameter wie Wachstumsrate, Sterblichkeit und Ähnliches zusammengefasst. Die zugehörige Differentialgleichung (DGLG) sieht folgendermaßen aus:

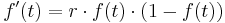
f'(t)=r\cdot f(t)\cdot(1-f(t))

Diese DGLG kann analytisch gelöst werden, was unterhalb für Dich durchgerechnet ist. Zur besseren Lesbarkeit wird statt 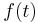\,f(t) einfach 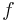\,fgeschrieben.

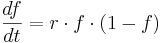
\frac{df}{dt}=r\cdot f\cdot (1-f)

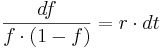
\frac{df}{f\cdot (1-f)}=r \cdot dt

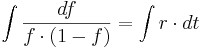
\int \frac{df}{f\cdot (1-f)}=\int r \cdot dt

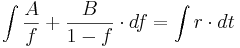
\int \frac{A}{f}+\frac{B}{1-f} \cdot df=\int r \cdot dt

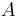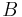Mittels Partialbruchzerlegung ermittelt man für \,A und \,B jeweils den Wert \,1 .

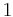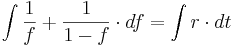
\int \frac{1}{f}+\frac{1}{1-f} \cdot df=\int r \cdot dt

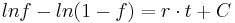
ln f - ln(1-f) = r\cdot t + C

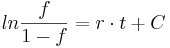
ln \frac{f}{1-f} = r\cdot t + C

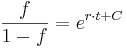
\frac{f}{1-f} = e^{r\cdot t + C}

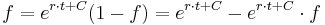
f = e^{r\cdot t + C}(1-f)=e^{r\cdot t + C}-e^{r\cdot t + C}\cdot f


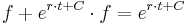
f+e^{r\cdot t + C}\cdot f = e^{r\cdot t + C}

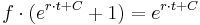
f\cdot(e^{r\cdot t + C}+1) = e^{r\cdot t + C}

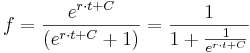
f = \frac{e^{r\cdot t + C}}{(e^{r\cdot t + C}+1)}=\frac{1}{1+\frac{1}{e^{r\cdot t + C}}}

Die Lösungsfunktion der logistischen DGLG lautet nun:

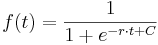
f(t)=\frac{1}{1+e^{-r\cdot t +C}}

Graph der Funktion in besserer Auflösung!
Graph der logistischen Funktion
(png-Datei, 5 kB)


Die Integrationskonstante 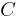\,C kann mittels der Anfangsbedingung 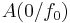\,A(0/f_{0}) ermittelt werden.

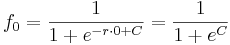
f_{0}=\frac{1}{1+e^{-r\cdot 0 +C}}=\frac{1}{1+e^{C}}

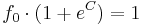
f_{0}\cdot(1+e^{C})=1

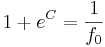
1+e^{C}=\frac{1}{f_{0}}

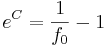
e^{C}=\frac{1}{f_{0}}-1

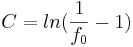
C=ln(\frac{1}{f_{0}}-1)

mit 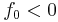\,f_{0}<0, da die maximale Population auf 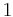\,1 normiert ist.

Die komplette Lösung lautet nun:

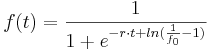
f(t)=\frac{1}{1+e^{-r\cdot t +ln(\frac{1}{f_{0}}-1)}}

Link:


Zurück zu Von der diskreten zur kontinuierlichen Veränderung

Von „http://medienvielfalt.zum.de/index.php?title=Logistisches_Wachstum_-_beschränktes_Wachstum&oldid=5793“