Quadratische Funktionen 2 - Allgemeine quadratische Funktion: Unterschied zwischen den Versionen
K |
|||
| (32 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | |
| + | [[Quadratische_Funktionen_2_Startseite|'''Startseite''']] - [[Quadratische_Funktionen_2_-_Bremsweg|'''1. Bremsweg''']] - [[Quadratische_Funktionen_2_-_Bremsbeschleunigung|'''2. Unterschiedliche Straßenverhältnisse''']] - [[Quadratische_Funktionen_2_-_Übungen1|'''3. Übungen 1''']] - [[Quadratische_Funktionen_2_-_Köln-Arena|'''4. Köln-Arena''']] - [[Quadratische_Funktionen_2_-_Einfluss_der_Parameter|'''5. Einfluss der Parameter in der Scheitelform''']] - <br>[[Quadratische_Funktionen_2_-_Übungen2|'''6. Übungen 2''']] - [[Quadratische_Funktionen_2_-_Allgemeine_quadratische_Funktion|'''7. Allgemeine quadratische Funktion''']] - [[Quadratische_Funktionen_2_-_Übungen3|'''8. Übungen 3''']] - [[Quadratische_Funktionen_2_-_Aufgaben|'''9. Aufgaben''']] | ||
| + | </div> | ||
| − | + | __NOCACHE__ | |
| − | Du kennst die [[quadratische_Funktionen_2_binomischen Formeln|binomische Formeln]]. | + | =Allgemeine quadratische Funktion mit den Parametern a, b und c= |
| − | <math>f(x) = a(x - d)^2 + e = a(x^2 - 2dx + d^2) + e = ax^2 - 2adx + ad^2 | + | |
| − | Vergleicht man diesen Term mit <math> f(x) = ax^2 + bx +c</math>, dann ist b = 2ad und <math>c = ad^2 - e</math>. | + | Du hast bisher kennengelernt, dass du eine quadratische Funktion in der Scheitelform <math>f: x \rightarrow a(x - d)^2 + e </math> schreiben kannst und in dieser Darstellung erkennst du die Scheitelkoordinaten S(d;e). |
| + | |||
| + | Meist werden quadratische Funktionen in der der Form <math>f: x \rightarrow ax^2 + bx +c</math> geschrieben. Auf dieser Seite soll nun der Zusammenhang zwischen beiden Darstellungen gewonnen und der Einfluss der Parameter a, b und c untersucht werden. | ||
| + | |||
| + | {{Merksatz|MERK= | ||
| + | Die <span style="background-color:yellow;">allgemeine quadratische Funktion</span> lautet | ||
| + | |||
| + | :<span style="background-color:yellow;"> '''<math> f: x\rightarrow ax^2 + bx + c </math>''' </span>. | ||
| + | |||
| + | Dabei sind <math>\ a, b, c </math> Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt <span style="background-color:yellow;"> '''<math>\ a,b,c \in R </math>''' </span> und <span style="background-color:yellow;"> '''<math>a\neq 0</math>''' </span>. | ||
| + | }} | ||
| + | |||
| + | ==Scheitelform in allgemeine Form== | ||
| + | |||
| + | Du kennst die [[quadratische_Funktionen_2_binomischen Formeln|binomische Formeln]]. Mit deren Hilfe kannst du den Term der Scheitelform <math> a(x - d)^2 + e</math> in den Term der allgemeinen quadratischen Funktion <math> ax^2 + bx + c</math> überführen. | ||
| + | |||
| + | Mit der 2. binomischen Formel ist <big><math>(x - d)^2</math></big> in <big><math>x^2 - 2dx + d^2</math></big>. Es ist dann | ||
| + | |||
| + | <big><math>f(x) = a(x - d)^2 + e = a(x^2 - 2dx + d^2) + e = ax^2 - 2adx + ad^2 + e</math></big> | ||
| + | |||
| + | Vergleicht man diesen Term mit <big><math> f(x) = ax^2 + bx +c</math></big>, dann ist <big><math>b = -2ad</math></big> und <big><math>c = ad^2 +e</math></big>. | ||
| + | |||
| + | ==Allgemeine Form in Scheitelform== | ||
| + | |||
| + | Umgekehrt kann man den Term <big><math> f(x) = ax^2 + bx +c</math></big> mittels [[Quadratische_Funktionen_2_-_quadratische_Ergänzung|quadratischer Ergänzung]] in den Term <big><math>a(x - d)^2 + e </math></big> überführen. Es ist dann <big><math> d = -\frac{b}{2a}</math></big> und <big><math>e = c - \frac{b^2}{4a}</math></big> | ||
| + | |||
| + | {{Aufgabe| | ||
| + | 1. Forme in die allgemeine Form um<br> | ||
| + | ::<math>2(x - 3)^2 + 1</math> | ||
| + | ::<math>\frac{1}{2}(x - 2)^2 - 2</math> | ||
| + | 2. Forme in die Scheitelform um<br> | ||
| + | ::<math>x^2 + 4x - 2</math> | ||
| + | ::<math>2x^2 + 3x + 2</math> | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1= | ||
| + | 1. | ||
| + | :<math>2x^2 - 12x + 19</math> | ||
| + | :<math>\frac{1}{2}x^2 - 2x</math> | ||
| + | 2. | ||
| + | :<math>(x + 2)^2 - 6</math> | ||
| + | :<math>2(x + \frac{3}{4})^2 + \frac{7}{8}</math> | ||
| + | }} | ||
| + | |||
| + | =Einfluss der Parameter a, b, c= | ||
| − | |||
Du kannst hier nun den '''Einfluss der Parameter a, b und c''' in der Funktion <math> f</math> mit <math> f(x) = ax^2 + bx + c</math> untersuchen. | Du kannst hier nun den '''Einfluss der Parameter a, b und c''' in der Funktion <math> f</math> mit <math> f(x) = ax^2 + bx + c</math> untersuchen. | ||
| Zeile 58: | Zeile 103: | ||
{{Merksatz|MERK= | {{Merksatz|MERK= | ||
| − | Die <span style="background-color:yellow;">allgemeine quadratische Funktion</span> lautet | + | 1. Die <span style="background-color:yellow;">allgemeine quadratische Funktion</span> lautet |
:<span style="background-color:yellow;"> '''<math> x\rightarrow ax^2 + bx + c </math>''' </span>. | :<span style="background-color:yellow;"> '''<math> x\rightarrow ax^2 + bx + c </math>''' </span>. | ||
| − | Dabei sind <math>\ a,b,c | + | Dabei sind <math>\ a, b, c </math> Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt <span style="background-color:yellow;"> '''<math>\ a,b,c \in R </math>''' </span> und <span style="background-color:yellow;"> '''<math>a\neq 0</math>''' </span>. |
| + | |||
| + | 2. Der allgemeinste Fall einer quadratischen Funktion hat also die Funktionsgleichung <big>f(x)=ax<sup>2</sup>+bx+c</big> }} | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="150"| | ||
| + | |width=20px| | ||
| + | |valign="top"; width=700px| | ||
| + | |||
| + | |||
| + | |} | ||
| + | |||
| + | {|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="200"| | ||
| + | {{Arbeiten| | ||
| + | NUMMER=1| | ||
| + | ARBEIT= | ||
| + | Experimentiere mit dem Applet und erläutere, welchen Einfluss die Parameter a, b und c auf den Verlauf des Graphen haben. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | #<span style="color: red">a bestimmt die Weite und die Öffnung nach oben und unten</span><br /> | ||
| + | #<span style="color: blue">b verschiebt den Scheitel</span><br /> | ||
| + | #<span style="color: green">c verschiebt den Scheitel für '''c > 0 nach oben''' und für '''c < 0 nach unten'''</span><br /> | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | |width=20px| | ||
| + | |valign="top"| | ||
| + | <ggb_applet height="400" width="650" filename="Allg_quadr_Fkt.ggb" /> | ||
| + | |} | ||
| + | |||
| + | {|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="200"| | ||
| + | {{Arbeiten| | ||
| + | NUMMER=2| | ||
| + | ARBEIT= | ||
| + | Stelle die drei Schieberegler so ein, dass der schwarze Graph genau auf dem | ||
| + | #roten | ||
| + | #grünen | ||
| + | #blauen | ||
| + | |||
| + | Graphen liegt. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | #<span style="color: blue">a = 0,5; b = 2,4; c = - 1</span><br /> | ||
| + | #<span style="color: red">a = - 1; b = -3; c = 2</span><br /> | ||
| + | #<span style="color: green">a = 0,5; b = - 2,4; c = - 1</span><br /> | ||
| + | }} | ||
| + | |||
| + | }} | ||
| + | |||
| + | |width=20px| | ||
| + | |valign="top"| | ||
| + | <ggb_applet height="500" width="650" filename="Quadratisch_allgemein2.ggb" /> | ||
| + | |} | ||
| + | |||
| + | |||
| + | {|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="930"| | ||
| + | {{Arbeiten| | ||
| + | NUMMER=3| | ||
| + | ARBEIT= | ||
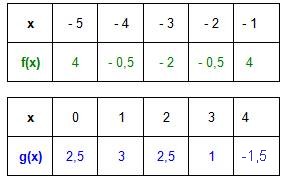
| + | Untersuche nun die Funktionen f mit '''f(x) = 1,5x<sup>2</sup> + 9x + 11,5''' und g mit '''g(x) = -0,5x<sup>2</sup> + x + 2,5''' | ||
| + | #Zeichne mit Hilfe einer Wertetabelle die Graphen G<sub>f</sub> und G<sub>g</sub> in ein gemeinsames Koordinatensystem. | ||
| + | #Gib die Koordinaten der beiden Scheitel S<sub>f</sub> und S<sub>g</sub> an. | ||
| + | #Vergleiche die beiden Parabeln mit der Normalparabel. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
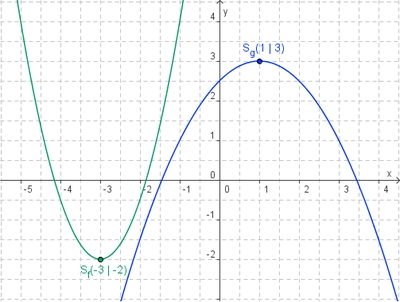
| + | #[[Bild:Quadratisch_Wertetabelle.jpg]] [[Bild:Quadratisch_allgemein3.jpg]] | ||
| + | #<span style="color: green">Scheitel von f: '''S(-3/-2)'''</span>; <span style="color: blue">Scheitel von g:''' S(1/3)'''</span> | ||
| + | #'''Parabel von f''': Enger als Normalparabel, nach oben geöffnet, verschoben | ||
| + | ::'''Parabel von g''': Weiter als Normalparabel, nach unten geöffnet, verschoben | ||
| + | }} | ||
| + | }} | ||
| + | |} | ||
| + | |||
| + | {{Merksatz|MERK= | ||
| + | Der Funktionsterm '''<math> ax^2 + bx + c </math>''' einer allgemeinen quadratischen Funktion '''<math> f: x\rightarrow ax^2 + bx + c </math>'''enthält einen <br> | ||
| + | reinquadratischen Teil '''<math>ax^2</math>''', einen linearen Teil '''<math>bx</math>''' und einen konstanten Teil '''<math>c</math>'''. }} | ||
| + | |||
| + | <br /> | ||
| + | |||
| + | ---- | ||
| + | {|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="120"|[[Bild:Maehnrot.jpg|100px]] | ||
| + | |align = "left"|'''Als nächstes kannst du prüfen, ob du alles verstanden hast.''' | ||
| + | [[Bild:Pfeil.gif]] [[Quadratische_Funktionen_2_-_Übungen3|'''Hier geht es weiter''']]'''.''' | ||
| + | |||
| + | |} | ||
---- | ---- | ||
| + | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| + | [[Quadratische_Funktionen_2_Startseite|'''Startseite''']] - [[Quadratische_Funktionen_2_-_Bremsweg|'''1. Bremsweg''']] - [[Quadratische_Funktionen_2_-_Bremsbeschleunigung|'''2. Unterschiedliche Straßenverhältnisse''']] - [[Quadratische_Funktionen_2_-_Übungen1|'''3. Übungen 1''']] - [[Quadratische_Funktionen_2_-_Köln-Arena|'''4. Köln-Arena''']] - [[Quadratische_Funktionen_2_-_Einfluss_der_Parameter|'''5. Einfluss der Parameter in der Scheitelform''']] - [[Quadratische_Funktionen_2_-_Übungen2|'''6. Übungen 2''']] - [[Quadratische_Funktionen_2_-_Allgemeine_quadratische_Funktion|'''7. Allgemeine quadratische Funktion''']] - [[Quadratische_Funktionen_2_-_Übungen3|'''8. Übungen 3''']] - [[Quadratische_Funktionen_2_-_Aufgaben|'''9. Aufgaben''']] | ||
Aktuelle Version vom 23. November 2016, 09:26 Uhr
Startseite - 1. Bremsweg - 2. Unterschiedliche Straßenverhältnisse - 3. Übungen 1 - 4. Köln-Arena - 5. Einfluss der Parameter in der Scheitelform -
6. Übungen 2 - 7. Allgemeine quadratische Funktion - 8. Übungen 3 - 9. Aufgaben
Inhaltsverzeichnis |
Allgemeine quadratische Funktion mit den Parametern a, b und c
Du hast bisher kennengelernt, dass du eine quadratische Funktion in der Scheitelform 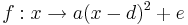 schreiben kannst und in dieser Darstellung erkennst du die Scheitelkoordinaten S(d;e).
schreiben kannst und in dieser Darstellung erkennst du die Scheitelkoordinaten S(d;e).
Meist werden quadratische Funktionen in der der Form 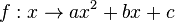 geschrieben. Auf dieser Seite soll nun der Zusammenhang zwischen beiden Darstellungen gewonnen und der Einfluss der Parameter a, b und c untersucht werden.
geschrieben. Auf dieser Seite soll nun der Zusammenhang zwischen beiden Darstellungen gewonnen und der Einfluss der Parameter a, b und c untersucht werden.
|
Merke:
Die allgemeine quadratische Funktion lautet
Dabei sind |
Scheitelform in allgemeine Form
Du kennst die binomische Formeln. Mit deren Hilfe kannst du den Term der Scheitelform 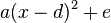 in den Term der allgemeinen quadratischen Funktion
in den Term der allgemeinen quadratischen Funktion 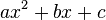 überführen.
überführen.
Mit der 2. binomischen Formel ist 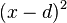 in
in 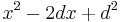 . Es ist dann
. Es ist dann
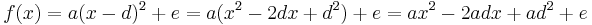
Vergleicht man diesen Term mit 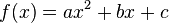 , dann ist
, dann ist 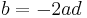 und
und 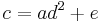 .
.
Allgemeine Form in Scheitelform
Umgekehrt kann man den Term 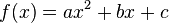 mittels quadratischer Ergänzung in den Term
mittels quadratischer Ergänzung in den Term 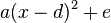 überführen. Es ist dann
überführen. Es ist dann 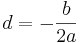 und
und 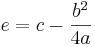
|
1. Forme in die allgemeine Form um 2. Forme in die Scheitelform um |
1.
2.
Einfluss der Parameter a, b, c
Du kannst hier nun den Einfluss der Parameter a, b und c in der Funktion  mit
mit 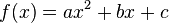 untersuchen.
untersuchen.
|
Hefteintrag: Am besten verwendest du hierfür dein Heft im Querformat, damit du eine Tabelle mit drei Spalten für den Einfluss von |
|
|
Du hast eine Menge über den Einfluss der einzelnen Parameter auf das Aussehen der Graphen herausgefunden. Natürlich können aber die Parameter nicht nur einzeln variiert werden, sondern auch mehrere oder alle gleichzeitig.
|
|
|
|
|
|
|
|
|
Merke:
Der Funktionsterm |

|
Als nächstes kannst du prüfen, ob du alles verstanden hast. |
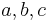 Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt
Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt 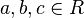
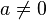
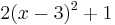
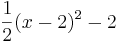
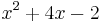
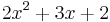
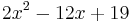
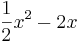
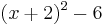
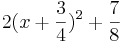
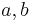 und
und  anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
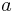
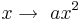 .
.
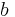
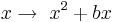 .
.
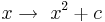 .
.
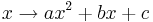
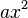 , einen linearen Teil
, einen linearen Teil 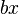 und einen konstanten Teil
und einen konstanten Teil  .
.

