Lösung zu Aufgabe B1
Lösung zu Aufgabe B1
|
<graphviz> digraph G { rankdir=LR; "Start"-> "|b| > 1"; "Start"-> "|b| < 1"; "|b| > 1"->"Stauchung in x-Richtung \n mit dem Faktor |1:b|"; "Stauchung in x-Richtung \n mit dem Faktor |1:b|" -> "b > 0"; "b > 0" -> "Ziel"; "Stauchung in x-Richtung \n mit dem Faktor |1:b|" -> "b < 0"; "b < 0" -> "Spiegelung an \n der y-Achse"; "Spiegelung an \n der y-Achse"-> "Ziel"; "|b| < 1"-> "Streckung in x-Richtung \n mit dem Faktor |1:b|"; "Streckung in x-Richtung \n mit dem Faktor |1:b|" -> "b > 0"; "Streckung in x-Richtung \n mit dem Faktor |1:b|" -> "b < 0"; } </graphviz>

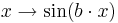
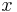 -Achse. Genauer:
-Achse. Genauer:
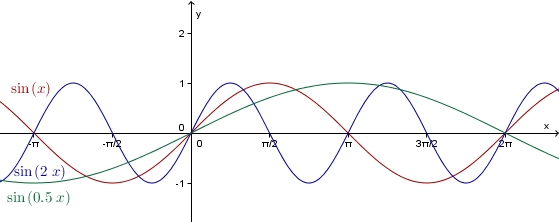
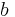 größer als eins, so wird der Graph der Sinusfunktion in
größer als eins, so wird der Graph der Sinusfunktion in  gestaucht.
gestaucht.
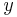 -Achse gespiegelt.
-Achse gespiegelt.
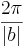 .
.