Potenzfunktionen - Einführung: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(→Der Graph der Funktion h(x) = a dot x3) |
(→Der Graph der Funktion h(x) = a \cdot x3) |
||
| Zeile 54: | Zeile 54: | ||
=== Verändern von Variablen === | === Verändern von Variablen === | ||
| − | ===Der Graph der Funktion h(x) = | + | ===Der Graph der Funktion <math>h(x) = a \cdot x^3</math>=== |
{| class="prettytable" | {| class="prettytable" | ||
| Zeile 61: | Zeile 61: | ||
filename="1_ax3.ggb" /> | filename="1_ax3.ggb" /> | ||
|| {{Arbeiten|NUMMER=5|ARBEIT= | || {{Arbeiten|NUMMER=5|ARBEIT= | ||
| − | Betätige den Schieberegler um die Variable a zu verändern. Beschreibe die Veränderung der Graphen der Funktion | + | Betätige den Schieberegler um die Variable a zu verändern. Beschreibe die Veränderung der Graphen der Funktion <math>f_a= a \cdot x^3</math> in Abhängigkeit von a! |
}} | }} | ||
|} | |} | ||
Version vom 8. Dezember 2008, 18:15 Uhr
Inhaltsverzeichnis |
Einführung
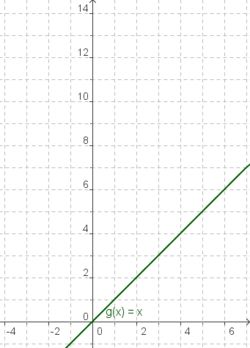
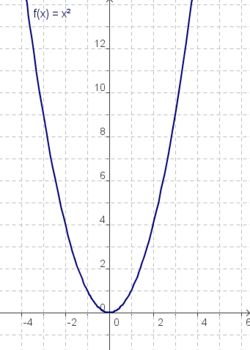
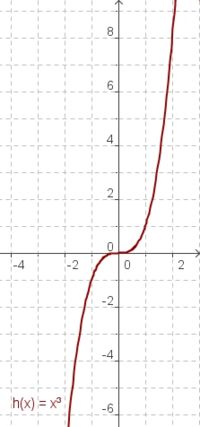
Die Graphen der Funktionen x, x² und x³
 |
 |
| ||
| g(x) = x | f(x) = x² | h(x) = x³ |
Aufgabe 1
|
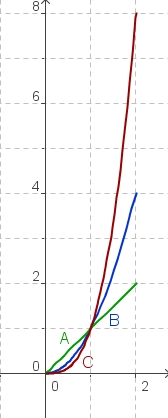
Die Graphen und ein Wanderer
Aufgabe 2
|
Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2
 |
g(x) = x (Graph A) f(x) = x2 (Graph B) | |||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
|
Verändern von Variablen
Der Graph der Funktion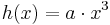 
|
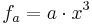in Abhängigkeit von a!
|
