Potenzfunktionen - Einführung: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 5: | Zeile 5: | ||
== Einführung== | == Einführung== | ||
== Die Graphen der Funktionen x, x² und x³== | == Die Graphen der Funktionen x, x² und x³== | ||
| − | {| class="prettytable" | + | {| class="prettytable" cellspacing="10" |
|- | |- | ||
| [[Bild:graphx.jpg |250px]] ||<br> || [[Bild:xhoch2.jpg |250px]] ||<br> ||[[Bild:graphxhoch3.jpg | 200px]] | | [[Bild:graphx.jpg |250px]] ||<br> || [[Bild:xhoch2.jpg |250px]] ||<br> ||[[Bild:graphxhoch3.jpg | 200px]] | ||
| Zeile 24: | Zeile 24: | ||
===Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2=== | ===Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2=== | ||
| − | {| class="prettytable" | + | {| class="prettytable" cellspacing="10" |
|- | |- | ||
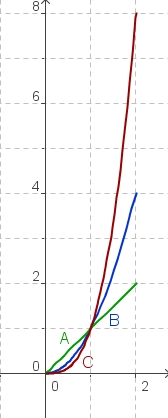
|rowspan=3|<br>|| rowspan=3|[[Bild:alle3graphen.jpg]]|| align="center"|'''g(x) = x (Graph A)'''<br><br> | |rowspan=3|<br>|| rowspan=3|[[Bild:alle3graphen.jpg]]|| align="center"|'''g(x) = x (Graph A)'''<br><br> | ||
'''f(x) = x<sup>2</sup> (Graph B)'''<br><br>'''h(x) = x<sup>3</sup> (Graph C)''' | '''f(x) = x<sup>2</sup> (Graph B)'''<br><br>'''h(x) = x<sup>3</sup> (Graph C)''' | ||
|- | |- | ||
| − | |align="left"| {{Arbeiten|NUMMER=3|ARBEIT= | + | |align="left" | {{Arbeiten|NUMMER=3|ARBEIT= |
# Begründe mit Hilfe der Tabelle, warum die '''Graphen A''' und '''B''' in der Umgebung des Nullpunktes stärker steigen als der '''Graph C'''. | # Begründe mit Hilfe der Tabelle, warum die '''Graphen A''' und '''B''' in der Umgebung des Nullpunktes stärker steigen als der '''Graph C'''. | ||
# Ab welchem Punkt steigt der '''Graph C''' stärker als der '''Graph A'''? | # Ab welchem Punkt steigt der '''Graph C''' stärker als der '''Graph A'''? | ||
| Zeile 59: | Zeile 59: | ||
===Der Graph der Funktion h<sub>a</sub>(x)<math>= a \cdot x^3</math> === | ===Der Graph der Funktion h<sub>a</sub>(x)<math>= a \cdot x^3</math> === | ||
| − | {| class="prettytable" | + | {| class="prettytable" cellspacing="10" |
|- | |- | ||
|<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true" | |<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true" | ||
| Zeile 71: | Zeile 71: | ||
===Der Graph der Funktion h<sub>a,c</sub>(x)<math> = a \cdot x^3 + c</math>=== | ===Der Graph der Funktion h<sub>a,c</sub>(x)<math> = a \cdot x^3 + c</math>=== | ||
<br> | <br> | ||
| − | {| class="prettytable" | + | {| class="prettytable" cellspacing="10" |
|- | |- | ||
|<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true" | |<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true" | ||
Version vom 8. Dezember 2008, 18:39 Uhr
Inhaltsverzeichnis |
Einführung
Die Graphen der Funktionen x, x² und x³
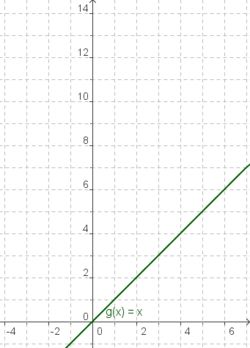 |
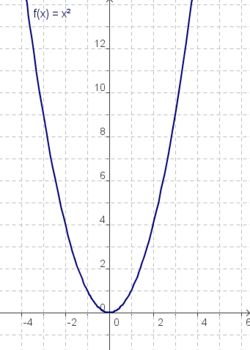 |
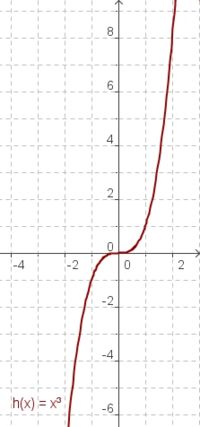
| ||
| g(x) = x | f(x) = x² | h(x) = x³ |
|
Die Graphen und ein Wanderer
|
Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2
Verändern von Variablen
Der Graph der Funktion ha(x)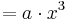
|
Der Graph der Funktion ha,c(x)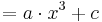
|
Teste Dein Wissen
Ordne die Funktionsterme den Funktionsgraphen zu!
|
Dieser Lernpfad wurde erstellt von:
Hans-Georg Weigand, Michael Schuster, Jan Wörlerund Petra Bader |
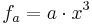 in Abhängigkeit von a!
in Abhängigkeit von a!


