Bestimmung der Funktionsgleichung aus dem Graphen: Unterschied zwischen den Versionen
(→Bestimmung einer Funktionsgleichung aus dem Graphen: Vorlage Video eingefügt) |
(→Informationen aus dem Graphen: Satzzeichen verbessert) |
||
| Zeile 22: | Zeile 22: | ||
# Gib die Nullstellen der Funktion an!<br> | # Gib die Nullstellen der Funktion an!<br> | ||
# An welchen Stellen sind die Funktionswerte am kleinsten und wo sind sie am größten? <br> | # An welchen Stellen sind die Funktionswerte am kleinsten und wo sind sie am größten? <br> | ||
| − | # Nenne jeweils einen Bereich in dem der Graph streng monoton fallend bzw. steigend ist | + | # Nenne jeweils einen Bereich in dem der Graph streng monoton fallend bzw. steigend ist! |
}} | }} | ||
||{{#ev:youtube|mSgduUqD_RE|150}} | ||{{#ev:youtube|mSgduUqD_RE|150}} | ||
Version vom 15. Februar 2009, 14:55 Uhr
Einführung - Station 1: Einfluss der Parameter - Station 2: Bestimmung der Funktionsgleichung und mehr - Station 3: Anwendungen in der Physik
Inhaltsverzeichnis |
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Hefteintrag: Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben!
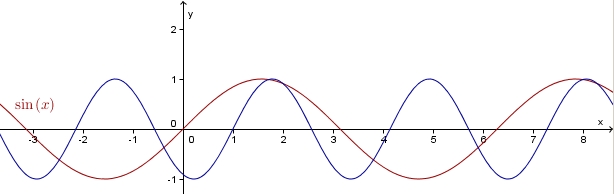
Informationen aus dem Graphen
|
|
|
Bestimmung einer Funktionsgleichung aus dem Graphen
|
|
Jetzt noch was zum Knobeln!!!
|
|
Super! Nun hast du es geschafft und das Ende der zweiten Station erreicht. Hefteintrag: Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alles Wichtige notiert hast! Falls du noch etwas üben möchtest, so löse die Zusatzaufgabe! |
Zusatzaufgabe
|
Lösung zu Aufgabe 1:
Amplitude: 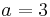
Wertemenge: ![W = [-3;\ 3]](/images/math/7/f/4/7f4a584468ac15313bbdcbd41602ca3e.png)
Periode: 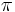
Nullstellen: 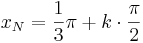 mit
mit  oder
oder 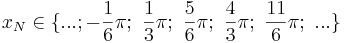
Tiefpunkte: 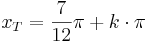 mit
mit  oder
oder 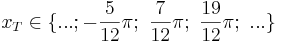
Hochpunkte: 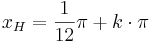 mit
mit  oder
oder 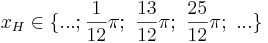
streng monoton fallend: ![...;\ [\frac{1}{12}\pi;\ \frac{7}{12}\pi];\ [\frac{13}{12}\pi;\ \frac{19}{12}\pi];\ ...](/images/math/2/3/5/2352ffad5112a215b1551af34791f362.png)
![...;\ [-\frac{5}{12}\pi;\ \frac{1}{12}\pi];\ [\frac{7}{12}\pi;\ \frac{13}{12}\pi];\ [\frac{19}{12}\pi;\ \frac{25}{12}\pi];\ ...](/images/math/a/b/3/ab3f03ffd65ea28a0ffd4a78e3cd5295.png)
Lösung zu Aufgabe 2: Hier kannst Du überprüfen, ob deine Ergebnisse stimmen. Stelle dazu die Schieberegler entsprechend ein.
Lösung zu Aufgabe 3:
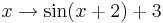 und
und 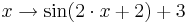
Lösung zu Aufgabe 4:
Nullstellen der Sinusfunktion: 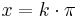 mit
mit  oder
oder 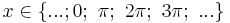
Nullstellen: 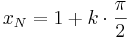 mit
mit  oder
oder 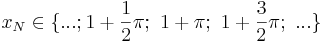
Hochpunkte: 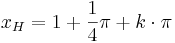 mit
mit  oder
oder 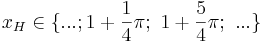
Tiefpunkte: 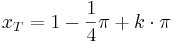 mit
mit  oder
oder 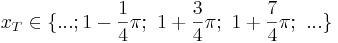
streng monoton fallend: ![...;\ [1+\frac{1}{4}\pi;\ 1+\frac{3}{4}\pi];\ [1+\frac{5}{4}\pi;\ 1+\frac{7}{4}\pi];\ ...](/images/math/3/8/c/38cede13d42a4986bf3d2217920545d4.png)
![...;\ [1-\frac{1}{4}\pi;\ 1+\frac{1}{4}\pi];\ [1+\frac{3}{4}\pi;\ 1+\frac{5}{4}\pi];\ ...](/images/math/9/d/1/9d17ad4a42698cc2f951c8cadb0f83ad.png)
Weiter geht es mit

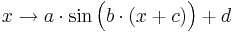 .
.