Potenzfunktionen - Einführung: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(→Der Graph der Funktion h(x) = a \cdot x^3) |
(→Die Graphen der Funktionen x, x² und x³) |
||
| (30 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Potenzfunktionen}} | |
| − | + | ||
== Einführung== | == Einführung== | ||
== Die Graphen der Funktionen x, x² und x³== | == Die Graphen der Funktionen x, x² und x³== | ||
| − | {| | + | {| cellspacing="10" |
|- | |- | ||
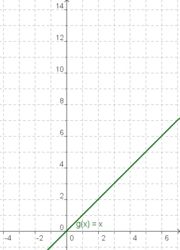
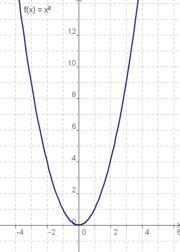
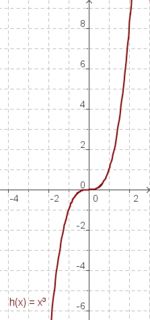
| − | | [[Bild:graphx.jpg | | + | | [[Bild:graphx.jpg |180px]] || [[Bild:xhoch2.jpg |180px]] ||[[Bild:graphxhoch3.jpg | 150px]] || {{Arbeiten|NUMMER=1|ARBEIT= |
| − | | | + | # Vergleiche den Graph der Funktion h(x) = x<sup>3</sup> mit dem Graphen der Funktion g(x) = x. Beschreibe Gemeinsamkeiten und Unterschiede! |
| − | | | + | |
| − | + | ||
| − | {{Arbeiten|NUMMER=1|ARBEIT= | + | |
| − | # Vergleiche den Graph der Funktion | + | |
# Vergleiche den Graph der Funktion mit h(x) = x<sup>3</sup> mit dem Graphen der quadratischen Funktion mit f(x) = x<sup>2</sup>. Beschreibe Gemeinsamkeiten und Unterschiede! | # Vergleiche den Graph der Funktion mit h(x) = x<sup>3</sup> mit dem Graphen der quadratischen Funktion mit f(x) = x<sup>2</sup>. Beschreibe Gemeinsamkeiten und Unterschiede! | ||
}} | }} | ||
| + | |- style="text-align:center;" | ||
| + | | '''g(x) = x''' || '''f(x) = x²''' || '''h(x) = x³''' | ||
| + | |} | ||
===Die Graphen und ein Wanderer=== | ===Die Graphen und ein Wanderer=== | ||
| − | {{Arbeiten|NUMMER=2|ARBEIT= | + | |
| − | # Ein Wanderer | + | |
| + | {| | ||
| + | |- | ||
| + | | {{Arbeiten|NUMMER=2|ARBEIT= | ||
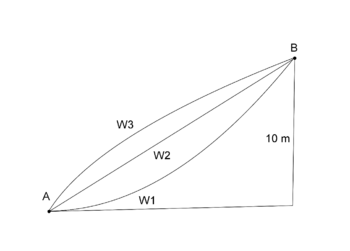
| + | # Ein Wanderer legt bei seinem Weg von A nach B einen Höhenunterschied von 10 m zurück. Wir betrachten nun drei verschiedene Formen des Verbindungsweges. Diese drei Wege haben im Seitenprofil in etwa die eingezeichneten Formen W<sub>1</sub>, W<sub>2</sub>, W<sub>3</sub>. Beschreibe den Wanderweg jeweils entlang dieser drei Wege, den der Wanderer zurücklegt, wenn er von A nach B geht.}} | ||
| + | | [[Bild:wanderer.png |350px]] | ||
| + | |} | ||
| + | |||
===Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2=== | ===Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2=== | ||
| − | {| | + | {|cellspacing="10" |
|- | |- | ||
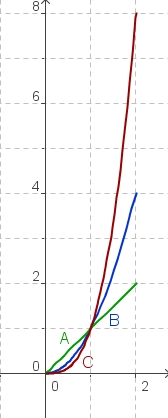
|rowspan=3|<br>|| rowspan=3|[[Bild:alle3graphen.jpg]]|| align="center"|'''g(x) = x (Graph A)'''<br><br> | |rowspan=3|<br>|| rowspan=3|[[Bild:alle3graphen.jpg]]|| align="center"|'''g(x) = x (Graph A)'''<br><br> | ||
'''f(x) = x<sup>2</sup> (Graph B)'''<br><br>'''h(x) = x<sup>3</sup> (Graph C)''' | '''f(x) = x<sup>2</sup> (Graph B)'''<br><br>'''h(x) = x<sup>3</sup> (Graph C)''' | ||
|- | |- | ||
| − | |align="left"| {{Arbeiten|NUMMER=3|ARBEIT= | + | |align="left" | {{Arbeiten|NUMMER=3|ARBEIT= |
# Begründe mit Hilfe der Tabelle, warum die '''Graphen A''' und '''B''' in der Umgebung des Nullpunktes stärker steigen als der '''Graph C'''. | # Begründe mit Hilfe der Tabelle, warum die '''Graphen A''' und '''B''' in der Umgebung des Nullpunktes stärker steigen als der '''Graph C'''. | ||
# Ab welchem Punkt steigt der '''Graph C''' stärker als der '''Graph A'''? | # Ab welchem Punkt steigt der '''Graph C''' stärker als der '''Graph A'''? | ||
| Zeile 34: | Zeile 39: | ||
|- | |- | ||
|align="center"| | |align="center"| | ||
| − | {| class="prettytable" | + | {| class="prettytable" |
|- | |- | ||
| '''x''' || '''Graph A''' || '''Graph B''' || '''Graph C''' | | '''x''' || '''Graph A''' || '''Graph B''' || '''Graph C''' | ||
| Zeile 55: | Zeile 60: | ||
== Verändern von Variablen == | == Verändern von Variablen == | ||
| − | ===Der Graph der Funktion h<sub>a</sub>(x) | + | ===Der Graph der Funktion h<sub>a</sub>(x)<math>= a \cdot x^3</math> === |
| − | {| | + | {| cellspacing="10" |
|- | |- | ||
|<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true" | |<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true" | ||
filename="1_ax3.ggb" /> | filename="1_ax3.ggb" /> | ||
|| {{Arbeiten|NUMMER=5|ARBEIT= | || {{Arbeiten|NUMMER=5|ARBEIT= | ||
| − | Betätige den Schieberegler um die '''Variable a''' zu verändern. Beschreibe die Veränderung der Graphen der Funktion <math>f_a= a \cdot x^3</math> in Abhängigkeit von a! | + | Betätige den Schieberegler um die '''Variable a''' zu verändern. Beschreibe die Veränderung der Graphen der Funktion mit <math>f_a= a \cdot x^3</math> in Abhängigkeit von a! |
| − | }} | + | }}<br> |
|} | |} | ||
| − | ===Der Graph der Funktion h<sub>a,c</sub>(x) | + | ===Der Graph der Funktion h<sub>a,c</sub>(x)<math> = a \cdot x^3 + c</math>=== |
<br> | <br> | ||
| − | {| | + | {| cellspacing="10" |
|- | |- | ||
|<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true" | |<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true" | ||
filename="2_ax3c.ggb" /> | filename="2_ax3c.ggb" /> | ||
|| {{Arbeiten|NUMMER=6|ARBEIT= | || {{Arbeiten|NUMMER=6|ARBEIT= | ||
| − | Verändere - mit dem Schieberegler - den Wert der '''Variablen c'''. Beschreibe! | + | Verändere - mit dem Schieberegler - den Wert der '''Variablen c'''. Beschreibe!}}<br> |
| − | }} | + | |
|} | |} | ||
==Teste Dein Wissen== | ==Teste Dein Wissen== | ||
| − | [http:// | + | [http://www.mathe-online.at/tests/fun1/erkennen.html Ordne die Funktionsterme den Funktionsgraphen zu! (auf www.mathe-online.at)] |
| + | |||
| + | [http://hotpotatoes.bildung-rp.de/parabel.htm Wähle den zum Graphen passenden Funktionsterm aus!] | ||
Aktuelle Version vom 17. Januar 2011, 08:50 Uhr
Inhaltsverzeichnis |
Einführung
Die Graphen der Funktionen x, x² und x³
Die Graphen und ein Wanderer
|
|
Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2
 |
g(x) = x (Graph A) f(x) = x2 (Graph B) | |||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
|
Verändern von Variablen
Der Graph der Funktion ha(x)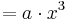
|
Der Graph der Funktion ha,c(x)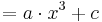
|
Teste Dein Wissen
Ordne die Funktionsterme den Funktionsgraphen zu! (auf www.mathe-online.at)
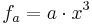 in Abhängigkeit von a!
in Abhängigkeit von a!

