Quadratische Funktionen Station3: Unterschied zwischen den Versionen
(→Merksatz: (Rein-)Quadratische Funktionen) |
(→Merksatz: (Rein-)Quadratische Funktionen) |
||
| Zeile 18: | Zeile 18: | ||
| − | === | + | === (Rein-)Quadratische Funktionen === |
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
| Zeile 29: | Zeile 29: | ||
NUMMER=4| | NUMMER=4| | ||
ARBEIT= | ARBEIT= | ||
| − | + | Nutze die Zeichnung rechts, um dieses Arbeitsblatt zu bearbeiten.}} | |
| − | + | <br> | |
| − | + | Das Applet zeigt den Graphen einer Funktion f mit '''f(x) = ax²'''. Hierbei steht a für eine beliebige reelle Zahl (<span style="color: darkred">nicht mehr für die Bremsbeschleunigung!</span>). | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Mit Hilfe des Schiebereglers (unten links im Applet) kannst du den Wert für a variieren. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|width=20px| | |width=20px| | ||
|valign="top"|<ggb_applet height="500" width="450" filename="Reinquadratisch.ggb" /> | |valign="top"|<ggb_applet height="500" width="450" filename="Reinquadratisch.ggb" /> | ||
| − | |||
| − | |||
| − | |||
|} | |} | ||
Version vom 27. März 2011, 15:11 Uhr
Nun wieder zurück zum Thema Bremsweg:
Wenn wir die bisherigen Überlegungen verallgemeinern wollen, müssen wir unsere Gleichung für den Bremsweg genauer analysieren.
Zunächst stellen wir fest, dass es eine funktionale Abhängigkeit des Bremsweges von der Geschwindigkeit gibt; wir können unsere Formel als Funktionsgleichung schreiben:
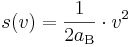. Die rechte Seite der Funktionsgleichung besteht aus dem Vorfaktor 
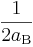und dem Quadrat der Variablen.
Besonders interessant ist dabei der Einfluss des Vorfaktors auf den Verlauf des Graphen:
Aufgabe 1
Wie ändert sich der Verlauf des Graphen, wenn der Vorfaktor von v2, d.h. wenn |
(Rein-)Quadratische Funktionen
| Die Funktionen, die wir bis jetzt betrachtet haben, weisen eine Gemeinsamkeit auf: Ihr Funktionsterm hat die Form ax². Sie zählen daher zu den quadratischen Funktionen. Die Graphen quadratischer Funktionen unterscheiden sich stark von den Graphen linearer Funktionen.
Mit Hilfe des Schiebereglers (unten links im Applet) kannst du den Wert für a variieren. |
|
