Numerische Näherung - Heronverfahren: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(→Numerische Näherung - Heronverfahren) |
|||
| Zeile 5: | Zeile 5: | ||
<math>x_{n+1}=\frac{x_{n}+\frac{a}{x_{n}}}{2}</math> | <math>x_{n+1}=\frac{x_{n}+\frac{a}{x_{n}}}{2}</math> | ||
| − | Den Startwert der Iteration kannst Du dabei beliebig positiv festsetzen. Versuche heraus zu finden, warum der Startwert <math> 0 </math> nicht in | + | Den Startwert der Iteration kannst Du dabei beliebig positiv festsetzen. Versuche heraus zu finden, warum der Startwert <math> 0 </math> nicht in Frage kommt! |
Derartige Rekursionen lassen sich mittels jeder Programmiersprache oder auch mit den Möglichkeiten eines Computer-Algebra-Systems (CAS) darstellen. Eine alternative Möglichkeit ist die Verwendung einer Tabellenkalkulation. | Derartige Rekursionen lassen sich mittels jeder Programmiersprache oder auch mit den Möglichkeiten eines Computer-Algebra-Systems (CAS) darstellen. Eine alternative Möglichkeit ist die Verwendung einer Tabellenkalkulation. | ||
Version vom 11. August 2011, 13:16 Uhr
Das Heron-Verfahren (auch babylonisches Wurzelziehen genannt) ist ein rekursives Näherungsverfahren zur Berechnung der Quadratwurzel einer Zahl, das von Heron von Alexandria erstmals beschreiben wurden.
Datei:Heron von Alexandria.jpg
Heron von Alexandria; Quelle: http://de.wikipedia.org
Die Iterationsvorschrift zur Berechnung der Wurzel aus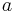 
(
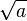) lautet:
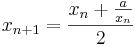
Den Startwert der Iteration kannst Du dabei beliebig positiv festsetzen. Versuche heraus zu finden, warum der Startwert 
nicht in Frage kommt!
Derartige Rekursionen lassen sich mittels jeder Programmiersprache oder auch mit den Möglichkeiten eines Computer-Algebra-Systems (CAS) darstellen. Eine alternative Möglichkeit ist die Verwendung einer Tabellenkalkulation.
Lösungsansätze:
- CAS am Beispiel der Open-Source-Software MAXIMA (Download unter http://maxima.sourceforge.net): Lösung mit Maxima (wxm-Datei, 2 kb)
- Tabellenkalkulation: Lösung mit Excel (xls-Datei, 25 kb)
