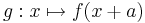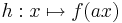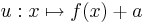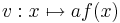Pool 2: Unterschied zwischen den Versionen
(→Transformation von Funktionen) |
(→Verhalten von Funktionen) |
||
| Zeile 37: | Zeile 37: | ||
Diskutiert das Verhalten und die Graphen der Funktionen | Diskutiert das Verhalten und die Graphen der Funktionen | ||
<math>\,g</math>, <math>\,h</math>, <math>\,u</math> und <math>\,v</math> | <math>\,g</math>, <math>\,h</math>, <math>\,u</math> und <math>\,v</math> | ||
| − | im Verhältnis zu jenen von <math>\,f</math>! Gebt einige Beispiele an und erstellt | + | im Verhältnis zu jenen von <math>\,f</math>! Gebt einige Beispiele an und erstellt aussagekräftige Grafiken! |
Wie übertragen sich folgende Eigenschaften auf die Funktionen <math>\,g</math>, <math>\,h</math>, <math>\,u</math> und <math>\,v</math>? | Wie übertragen sich folgende Eigenschaften auf die Funktionen <math>\,g</math>, <math>\,h</math>, <math>\,u</math> und <math>\,v</math>? | ||
Version vom 15. September 2008, 19:21 Uhr
Lernpfad zur Schnittstelle Sekundarstufe 2 - Universität
Aufgabenpool 2
Startseite des Lernpfads | Aufgabenpool 1 | Didaktischer Kommentar
Inhaltsverzeichnis |
Text korrigieren
[Aufgabe für 2er- oder 3er-Gruppe] [Franz]
xxx
Text korrigieren
[Aufgabe für 2er- oder 3er-Gruppe] [Matthias]
xxx
Text korrigieren
[Aufgabe für 2er- oder 3er-Gruppe] [Jochen]
xxx
Verhalten von Funktionen
[Aufgabe für 2er- oder 3er-Gruppe] [Franz]
Gegeben sei eine Funktion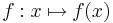 
. Ist 
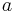eine Konstante, so können aus 
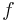weitere Funktionen gewonnen werden:
Diskutiert das Verhalten und die Graphen der Funktionen
, 
, 
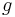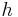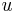und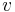 
im Verhältnis zu jenen von 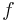! Gebt einige Beispiele an und erstellt aussagekräftige Grafiken!
Wie übertragen sich folgende Eigenschaften auf die Funktionen 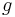, , 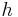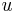und ?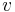
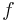- ist periodisch mit Periode
.
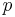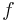- ist überall positiv.
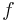- ist monoton steigend.
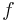- hat bei
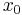eine Nullstelle (d.h. 
).
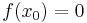Erstellt mit einem dynamischen Geometriesystem (z.B. GeoGebra) ein Arbeitsblatt, in dem anhand einer Funktion 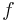eurer Wahl die Konstante 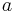mittels eines Schiebereglers variiert werden kann!
Das Integral
[Aufgabe für 2er- oder 3er-Gruppe] [Matthias]
Stichworte: Was ist das Integral? Unterschied bestimmtes Integral/unbestimmtes Integral (Stammfunktion).
Kurvendiskussion
[Aufgabe für 2er- oder 3er-Gruppe] [Jochen]
Stichworte: Hochpunkt, Tiefpunkt, Wendepunkt,... Was sind sie, wie finden wir sie und warum finden wir sie auf diese Weise?
Bewegung (fächerübergreifend mit Physik)
[Aufgabe für 2er- oder 3er-Gruppe] [Franz]
Was haben Zeit, Weg (Ort), Geschwindigkeit und Beschleunigung mit dem Differenzieren und Integrieren zu tun? Ihr könnt dabei davon ausgehen, dass eine Bewegungsform durch eine Zuordnung
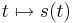
beschrieben wird. Dabei ist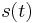 
der Ort des betrachteten Objekts zur Zeit 
.
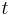Gebt einige Beispiele für Bewegungsformen an und erstellt aussagekräftige Grafiken oder Animationen (etwa mit einem Computeralgebra-System).
Beantwortet folgende Fragen:
- Kann die Geschwindigkeit als Funktion der Zeit erhalten werden, wenn der Ort als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Kann die Beschleunigung als Funktion der Zeit erhalten werden, wenn der Ort als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Kann die Beschleunigung als Funktion der Zeit erhalten werden, wenn die Geschwindigkeit als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Kann der Ort als Funktion der Zeit erhalten werden, wenn die Geschwindigkeit als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Kann der Ort als Funktion der Zeit erhalten werden, wenn die Beschleunigung als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Wie kann der Ort als Funktion der Zeit erhalten werden, wenn bekannt ist, dass die Beschleunigung konstant (
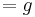) ist, und dass zur Zeit 
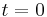sowohl der Ort als auch die Geschwindigkeit gleich 0 sind? (Kommt euch das Ergebnis bekannt vor?)
Kosten- und Preistheorie
[Aufgabe für 2er- oder 3er-Gruppe] [Peter]
Stichworte: Betriebsoptimale Menge, Carnotscher Punkt.
Funktionstypen
[Aufgabe für 2er- oder 3er-Gruppe] [Matthias]
Stichworte: Welche Typen von Funktionen gibt es, was sind ihre charakteristischen Eigenschaften? Die Beschreibung soll folgende Begriffe enthalten:
- Asymptoten
- Definitionsmenge
- exponential-
- logarithmisch
- periodisch
- Polstelle
- Polynom
- Symmetrie, symmetrisch
- Winkelfunktion
- Wurzel
