Pool 1
Lernpfad zur Schnittstelle Sekundarstufe 2 - Universität bzw. Hochschule
Aufgabenpool 1
Startseite des Lernpfads | Aufgabenpool 2 | Didaktischer Kommentar
Inhaltsverzeichnis |
Differentialgleichung versus Differenzengleichung
[Einzelaufgaben] (Walter Wegscheider und Matthias Kittel)
siehe Lernpfad Diskret - kontinuierlich
Integrationsverfahren vergleichen
[Aufgabe für 3er-Gruppe] (Matthias Kittel)
Die Berechnung von Integralen ist eine oft notwendige Operation, die in vielen Bereichen des (natur)wissenschaftlichen Lebens Anwendung findet. Gar nicht so selten kommt es vor, dass ein Integral gar nicht analytisch lösbar ist. Das bedeutet, es gibt kein Verfahren wie die partielle Integration, die Substitutionsmethode oder die Partialbruchzerlegung (diese Lösungswege lernst Du in der Schule, es gibt aber noch viel mehr), um das Integral lösen zu können. Aus diesem Grund ist es notwendig alternative Integrationsmethoden zu finden. Hier werden zwei Möglichkeiten vorgestellt:
- Die gegebene Funktion wird vereinfacht: Sie wird durch ein beliebig genaues Taylorpolynom angenähert. Bei diesem Verfahren sind nur Kenntnisse über das Ableiten notwendig. Jede (normale) Funktion ist ja bekanntlich differenzierbar, auch wenn es umständlich ist und lange dauert. Es wird die Formel
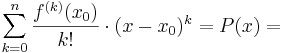
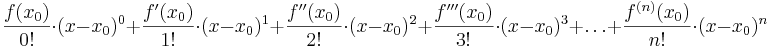
verwendet. Danach wird dieses Polynom 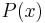 an Stelle der gegebenen Funktion
an Stelle der gegebenen Funktion 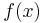 integriert.
integriert.
- Das Integral wird durch numerische Methoden angenähert: Man führt also keine analytische Integration durch, sondern nähert den Wert des Integrals durch Summen an. Hier gibt es einige Methoden, die je nach Aufwand zu genaueren oder weniger genaueren Ergebnissen führen. Die bekanntesten Verfahren sind:
Rechtecksformel: 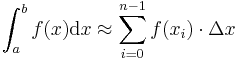 mit einer Schrittweite
mit einer Schrittweite 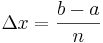 , wobei
, wobei 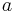 und
und 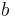 die untere und obere Grenze des Integrals darstellt.
die untere und obere Grenze des Integrals darstellt. 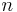 gibt die Anzahl der Rechtecke an, in die die Fläche unterhalb der Funktion zerlegt wird. Möchte man das Intervall
gibt die Anzahl der Rechtecke an, in die die Fläche unterhalb der Funktion zerlegt wird. Möchte man das Intervall ![\, [2;3]](/images/math/3/3/5/335abc90babc4c3c7d7c5b397b562b1d.png) in
in 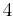 Rechtecke unterteilen, erhält man
Rechtecke unterteilen, erhält man 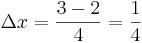 und die Stützstellen
und die Stützstellen 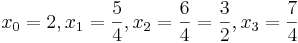 .
.
Trapezformel: 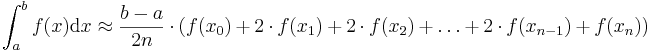 mit
mit 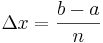 , wobei
, wobei 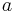 und
und 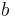 die untere und obere Grenze des Integrals darstellt. Je größer hier
die untere und obere Grenze des Integrals darstellt. Je größer hier 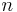 ist, desto genauer wird das Ergebnis. Die einzelnen
ist, desto genauer wird das Ergebnis. Die einzelnen 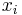 werden wie oben berechnet. Das gewählte
werden wie oben berechnet. Das gewählte 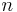 wird dann einfach in die Formel eingesetzt.
wird dann einfach in die Formel eingesetzt.
Simpson'sche Formel: 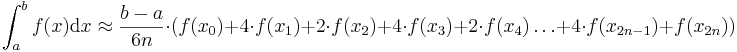 mit
mit 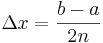 , wobei
, wobei 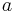 und
und 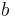 die untere und obere Grenze des Integrals darstellt. Für
die untere und obere Grenze des Integrals darstellt. Für 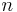 und die
und die 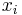 gilt Obiges.
gilt Obiges.
|
Gegeben ist die Funktion Bearbeitet folgende Arbeitspunkte. Jeder Schüler sucht sich zwei Punkte aus:
|
Aufgaben im pdf-Format
Die Angaben zu den Aufgaben findet man unter Integrationsmethoden_mv.pdf (41 kb).
Lösungen im pdf-Format
Die Lösungen zu diesen Aufgaben findet man unter Lösungen zu Integrationsmethoden_mv.pdf (117 kb).
Logistische Abbildung/Gleichung - Ein-Lebewesen-Modell nach Verhulst
[Aufgabe für 2er-Gruppe] (Matthias Kittel)
Das Verhalten einer Population von Lebewesen lässt sich mit Hilfe der logistischen Gleichung leicht visualisieren. Diese Gleichung lässt sich etweder analytisch oder mittels Differenzengleichung lösen.
Die logistischen Gleichung beschreibt ein Wachstum mit einer Grenzpopulation, das bedeutet, dass sich die Population nicht auf alle Zeiten exponentiell vermehrt, sondern sich einer Maximalpopulation annähert. Neben der Geburtenrate 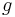 fließt die natürliche Sterberate
fließt die natürliche Sterberate 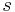 (Alter, Krankheit und Ähnliches) und die Sterberate auf Grund von Überbevölkerung
(Alter, Krankheit und Ähnliches) und die Sterberate auf Grund von Überbevölkerung 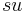 (fehlender Lebensraum, Nahrungsmittelknappheit, etc.) in die Gleichung mit ein.
Die Änderung der Populationszahl
(fehlender Lebensraum, Nahrungsmittelknappheit, etc.) in die Gleichung mit ein.
Die Änderung der Populationszahl 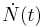 mit der Zeit lässt sich nun wie folgt berechnen:
mit der Zeit lässt sich nun wie folgt berechnen:
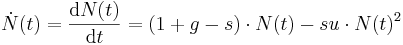
Die Lösung dieser Differentialgleichung lautet:
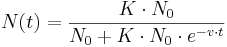 , wobei
, wobei 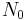 die Anfangspopulation ist und
die Anfangspopulation ist und 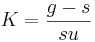 sowie
sowie 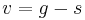 gilt.
gilt.
Die entsprechende Differenzengleichung lautet:
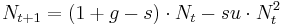 .
.
Die analytische Lösung, sowie die Lösung der Differenzengleichung sind in dem
Excel-Arbeitsblatt zum Ein-Lebewesen-Modell nach Verhulst (1,4Mb) programmiert und graphisch dargestellt. Es lassen sich die Anzahl der Individuen, sowie die Parameter 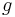 ,
, 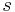 und
und 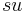 eingeben. Die Differenzengleichung wird für die ersten
eingeben. Die Differenzengleichung wird für die ersten 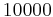 Schritte gelöst und gemeinsam mit der analytischen Lösung in einem Graphen für die ersten
Schritte gelöst und gemeinsam mit der analytischen Lösung in einem Graphen für die ersten 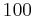 Schritte dargestellt. Des Weiteren wird noch der Grenzwert der Population und der Chaosparamter
Schritte dargestellt. Des Weiteren wird noch der Grenzwert der Population und der Chaosparamter 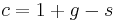 berechnet. Es können mit diesem Excel-Arbeitsblatt auch eigene Graphen erstellt und selbstständig Rechnungen durchgeführt werden.
berechnet. Es können mit diesem Excel-Arbeitsblatt auch eigene Graphen erstellt und selbstständig Rechnungen durchgeführt werden.
Die Differenzengleichung liefert je nach Wert dieses Chaosparameters von einander stark abweichende Lösungen.
Folgendes Verhalten der logistischen Gleichung kann in Abhängigkeit des Parameters 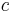 beobachtet werden:
beobachtet werden:
-
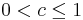 - Die Population stirbt aus, die Anzahl der Individuen nimmt exponentiell ab.
- Die Population stirbt aus, die Anzahl der Individuen nimmt exponentiell ab.
-
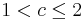 - Die Population wächst bis sie die Grenzpopulation erreicht.
- Die Population wächst bis sie die Grenzpopulation erreicht.
-
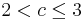 - Die Pupulation wächst und die Anzahl der Individuen schwingt um die Grenzpopulation und nähert sich dieser wie eine gedämpfte Schwingung. Je näher der Parameter bei dem Wert
- Die Pupulation wächst und die Anzahl der Individuen schwingt um die Grenzpopulation und nähert sich dieser wie eine gedämpfte Schwingung. Je näher der Parameter bei dem Wert 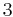 , desto länger dauert dieser Schwingvorgang.
, desto länger dauert dieser Schwingvorgang.
-
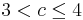 - Die Population pendelt zwischen mehreren Werten (im Intervall
- Die Population pendelt zwischen mehreren Werten (im Intervall ![\, [3 ; 3,45]](/images/math/0/0/1/0016067739b404503dc581e427cde65c.png) zwischen zwei Werten bei
zwischen zwei Werten bei 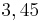 zwischen vier Werten usw.) und erreicht ab ungefähr
zwischen vier Werten usw.) und erreicht ab ungefähr 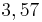 chaotisches Verhalten. Das heißt, dass die Anzahl der Individuen nicht mehr vorhergesagt werden kann bzw. kleine Änderungen in den Parametern zu großen Änderungen in den Ergebnissen führen.
chaotisches Verhalten. Das heißt, dass die Anzahl der Individuen nicht mehr vorhergesagt werden kann bzw. kleine Änderungen in den Parametern zu großen Änderungen in den Ergebnissen führen.
|
Führt selbst eine Parameterstudie durch und überprüft oben angegebene Intervalle des Chaosparameters auf ihre Richtigkeit. Welche weiteren überraschenden Ergebnisse liefert die logistischen Gleichung? Experimentiert mit dem Excel-Arbeitsblatt. Verwende dazu die Angabe aus dem pdf-file Arbeitsblatt Parameterstudie zum Ein-Lebewesen-Modell nach Verhulst (40kb). Fertigt ein Protokoll an, in dem eure Experimente dokumentiert sind! Fertigt so viele Graphen wie möglich an! Unter Die logistische Differentialgleichung findet man noch weitere Übungsaufgaben und einen Graphenplotter, der online Graphen für unterschiedliche Parameterwerte zeichnet. |
Link:
- Günther Ossimitz, Zwei Zugänge zum logistischen Wachstum, Univ. Klagenfurt - Betrachtungen und Herleitung der logistischen Differentialgleichung.
Räuber-Beute-Modell
|
Als Erweiterung dieses Beispieles kann das Räuber-Beute-Modell gesehen werden. Ein Modell, das die Abhängigkeit der Population eines Beutetieres (Hase) und eines Raubtieres (Fuchs) voneinander untersucht. Hier gelten die Lotka-Volterra-Regeln:
Im Excel-Arbeitsblatt zum Räuber-Beute-Modell (3,6Mb) werden wiederum die Population berechnet und die Ergebnisse graphisch visualisiert. Auch hier können alle Parameter variiert werden, um obige Gesetze zu verifizieren. Alle Bedienungshinweise sind in der Datei angegeben. |
Ein bisschen Relativitätstheorie
[Aufgabe für 2er-Gruppe] (Franz Embacher)
Die Funktion
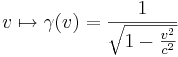
spielt in der Speziellen Relativitätstheorie eine wichtige Rolle. Die Variable 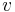 steht für die Geschwindigkeit, mit der sich ein Körper (relativ zu einem Bezugssystem) bewegt, die Konstante
steht für die Geschwindigkeit, mit der sich ein Körper (relativ zu einem Bezugssystem) bewegt, die Konstante 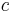 bezeichnet die Lichtgeschwindigkeit.
Bearbeitet zunächst getrennt folgende Fragestellungen:
bezeichnet die Lichtgeschwindigkeit.
Bearbeitet zunächst getrennt folgende Fragestellungen:
- a.) Wie verhält sich die gegebene Funktion für Geschwindigkeiten
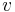 , deren Betrag sehr viel kleiner als die Lichtgeschwindigkeit sind (
, deren Betrag sehr viel kleiner als die Lichtgeschwindigkeit sind ( )? Erstelle eine Näherungsformel
)? Erstelle eine Näherungsformel 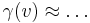 (Reihenentwicklung bis zur Ordnung
(Reihenentwicklung bis zur Ordnung 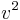 )! Wie sieht der Graph der Funktion in diesem Bereich aus?
)! Wie sieht der Graph der Funktion in diesem Bereich aus?
- b.) Wie verhält sich die gegebene Funktion für Geschwindigkeiten
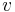 , die in der Nähe der Lichtgeschwindigkeit liegen (
, die in der Nähe der Lichtgeschwindigkeit liegen (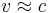 , wobei aber
, wobei aber 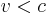 sein soll)? Erstelle eine Näherungsformel
sein soll)? Erstelle eine Näherungsformel 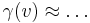 ! Hier ein Tipp:
! Hier ein Tipp: 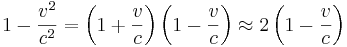 .
.
Setzt euch danach wieder zusammen, diskutiert eure Ergebnisse und führt sie zusammen:
- Wie sieht der Graph der gesamten Funktion aus? (Welche Definitionsmenge wird man sinnvollerweise für sie wählen?)
- Wie passt dieser Graph mit den Graphen der (von euren getrennt erhaltenen) Näherungsfunktionen zusammen? Stellt alle drei Graphen in einem Diagramm dar! Verwendet als Tool einen Funktionsplotter oder ein Programm, das einen solchen enthält! Überlegt euch, wie ihr die Einheiten auf den Achsen wählt, damit das Diagramm möglichst aussagekräftig wird!
- Illustriert anhand einiger Werte von
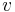 (z.B. die Geschwindigkeit eines Fußgängers, eines Flugzeugs, 90% der Lichtgeschwindigkeit, 99% der Lichtgeschwindigkeit...) wie gut eure Näherungsformeln sind!
(z.B. die Geschwindigkeit eines Fußgängers, eines Flugzeugs, 90% der Lichtgeschwindigkeit, 99% der Lichtgeschwindigkeit...) wie gut eure Näherungsformeln sind!
Wenn das alles geklärt ist, könnt ihr ein bisschen Relativitätstheorie betreiben:
- Die (relativistische) Gesamtenergie eines Körpers der Masse
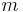 , der sich mit der Geschwindigkeit
, der sich mit der Geschwindigkeit 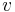 bewegt, ist durch
bewegt, ist durch 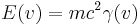 gegeben. Wie verhält sich
gegeben. Wie verhält sich 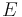 für kleine Geschwindigkeiten? Erinnert euch das Ergebnis an etwas, das ihr in eurem Physikunterricht gelernt habt? Wie verhält sich
für kleine Geschwindigkeiten? Erinnert euch das Ergebnis an etwas, das ihr in eurem Physikunterricht gelernt habt? Wie verhält sich 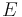 für große Geschwindigkeiten? (Damit könnt ihr argumentieren, dass kein Körper auf Lichtgeschwindigkeit beschleunigt werden kann!)
für große Geschwindigkeiten? (Damit könnt ihr argumentieren, dass kein Körper auf Lichtgeschwindigkeit beschleunigt werden kann!)
- Zwillingsparadoxon: Alice und Bob sich gleich alt. Alice unternimmt eine Reise durchs All mit Geschwindigkeit
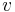 , während Bob auf der Erde zurückbleibt. Als Alice zurückkehrt, stellen die beiden fest, dass Alice jünger geblieben ist. Ist für Bob die Zeit
, während Bob auf der Erde zurückbleibt. Als Alice zurückkehrt, stellen die beiden fest, dass Alice jünger geblieben ist. Ist für Bob die Zeit 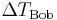 vergangen und für Alice die Zeit
vergangen und für Alice die Zeit 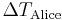 , so ist sagt die Relativitätstheorie die Beziehung
, so ist sagt die Relativitätstheorie die Beziehung 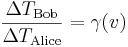
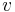 abgeschätzt werden kann!
abgeschätzt werden kann!
Epidemie
[Aufgabe für 2er-Gruppe] (Peter Hofbauer)
Jährlich wird Europa von Grippewellen überrollt, die trotz der Möglichkeit der Grippeimpfung immer wieder zahlreiche Todesfälle fordern.
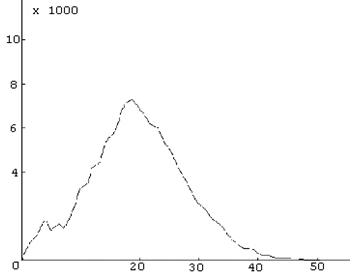
In der nachfolgenden Abbildung seht ihr den Tagesreport der Grippefälle einer Kleinstadt. Waagrecht sind die Tage ab Ausbruch der Grippewelle aufgetragen, senkrecht die Anzahl der an der Grippe erkrankten Personen an diesem Tag:
Setzt euch zusammen und überlegt vorerst ganz allgemein (d.h. ohne jetzt schon Berechnungen anzustellen), wie sich die folgenden Fragen mathematisch behandeln und beantworten lassen:
- Welche Funktionen könnten geeignet sein, um den Epidemieverlauf zu modellieren?
- Welche Aussagekraft hat die 1. Ableitung dieser Modellfunktion?
- Wie lässt sich das Integral dieser Funktion aus volkswirtschaftlicher Sicht interpretieren?
- Zu welchem Zeitpunkt verbreitete sich die Krankheit am stärksten?
- Wann begann die Anzahl der Neuinfektionen rückläufig zu werden?
Geht jetzt auseinander und versucht jeder alleine eine Modellfunktion zu finden und die oben gestellten Fragen mithilfe dieser Funktion zu beantworten. Die Daten müsst ihr aus der Grafik ablesen.
Vergleicht anschließend eure Ergebnisse. Wahrscheinlich werdet ihr nicht zu denselben Ergebnissen gekommen sein, dennoch solltet ihr zu ähnlichen Schlüssen kommen.
Diskutiert abschließend die Frage, welche Informationen notwendig wären um mithilfe des Integrals die Frage beantworten zu können, ob eine kostenlose Grippeimpfung volkswirtschaftlich sinnvoll wäre.
Elastizität
[Aufgabe für 2er- oder 3er-Gruppe] (Peter Hofbauer)
Der Begriff der Elastizität ist in der Ökonomie von entscheidender Bedeutung.
Die Elastizität einer Funktion f(x) an der Stelle x0 ist definiert durch: 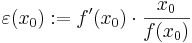
Eine Motivation für diesen Begriff und einige Erklärungen dazu findest du unter anderem auf folgenden Seiten:
- Wikipedia (betrachte dabei nur den Fall mit einer Variablen!)
- Foliensatz von Josef Leydold (Wirtschaftsuniversität Wien) (kannst du das Beispiel am Ende der Seite nachvollziehen?)
- Eine ausgezeichnete Erklärung dafür, warum Cola an Flughäfen so teuer ist, liefert die Frankfurter Allgemeine Zeitung mithilfe der Elastizität .
|
Macht euch zuerst anhand der oben angeführten Links alleine mit dem Begriff der Elastizität ein wenig vertraut und setzt euch anschließend zusammen und versucht folgende Fragen zu beantworten:
|
Rekursionsverfahren
[Einzelaufgaben] (Walter Wegscheider und Matthias Kittel)
siehe Lernpfad Diskret - kontinuierlich
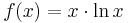 . Es gilt
. Es gilt 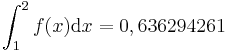 FE.
FE.
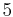 )! Welche Auswirkung hat die Erhöhung der Rechteckanzahl auf die Genauigkeit des Ergebnisses?
)! Welche Auswirkung hat die Erhöhung der Rechteckanzahl auf die Genauigkeit des Ergebnisses?
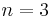 )!
)!
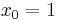 !
!
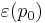 ?
?

