Zum Nachschlagen: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
K (→Zum Nachschlagen) |
(Navigation) |
||
| (11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Trigonometrische Funktionen}} | |
| − | + | ||
| − | + | ||
| Zeile 22: | Zeile 20: | ||
:* Frequenz <math>\ f</math> {{versteckt|::Als Frequenz <math>\ f</math> bezeichnet man die Anzahl der durchlaufenen Schwingungsperioden pro Zeitintervall. Ihre Einheit ist Hertz (abgekürzt Hz). Werden beispielsweise 50 Schwingungsperioden pro Sekunde durchlaufen, so sagt man, die Schwingung hat 50 Hz. | :* Frequenz <math>\ f</math> {{versteckt|::Als Frequenz <math>\ f</math> bezeichnet man die Anzahl der durchlaufenen Schwingungsperioden pro Zeitintervall. Ihre Einheit ist Hertz (abgekürzt Hz). Werden beispielsweise 50 Schwingungsperioden pro Sekunde durchlaufen, so sagt man, die Schwingung hat 50 Hz. | ||
| − | ::Es gilt: <math>f = \frac{1}{T}</math>}} | + | ::Es gilt: <math>f = \frac{1}{T}</math> |
| + | ::( <math>\ T </math> Schwingungsdauer)}} | ||
:* Hochpunkt {{versteckt|::Ein Hochpunkt einer Funktion <math>\ f</math> ist eine Stelle <math>\ x</math>, an der <math>\ f</math> größere Werte besitzt als an allen anderen Stellen einer kleinen Umgebung von <math>\ x</math>.}} | :* Hochpunkt {{versteckt|::Ein Hochpunkt einer Funktion <math>\ f</math> ist eine Stelle <math>\ x</math>, an der <math>\ f</math> größere Werte besitzt als an allen anderen Stellen einer kleinen Umgebung von <math>\ x</math>.}} | ||
| Zeile 29: | Zeile 28: | ||
:* Kosinuskurve {{versteckt|::Der Graph der Kosinusfunktion wird Kosinuskurve genannt.}} | :* Kosinuskurve {{versteckt|::Der Graph der Kosinusfunktion wird Kosinuskurve genannt.}} | ||
| − | |||
| − | |||
:* Monotonie {{versteckt|::Eine Funktion heißt streng monoton wachsend, wenn sie an größeren Stellen größere Werte besitzt. Eine Funktion heißt streng monoton fallend, wenn sie an größeren Stellen kleinere Werte besitzt. Eine Funktion kann in manchen Intervallen streng monoton wachsend und in anderen Intervallen streng monton fallend sein - beispielsweise bei Schwingungen!}} | :* Monotonie {{versteckt|::Eine Funktion heißt streng monoton wachsend, wenn sie an größeren Stellen größere Werte besitzt. Eine Funktion heißt streng monoton fallend, wenn sie an größeren Stellen kleinere Werte besitzt. Eine Funktion kann in manchen Intervallen streng monoton wachsend und in anderen Intervallen streng monton fallend sein - beispielsweise bei Schwingungen!}} | ||
| Zeile 38: | Zeile 35: | ||
:* Periode {{versteckt|::Der Abstand zweier Orte im gleichen Schwingungszustand wird als Periode bezeichnet. Die Periode der Sinus- und Kosinusfunktion beträgt jeweils <math>2\pi</math>.}} | :* Periode {{versteckt|::Der Abstand zweier Orte im gleichen Schwingungszustand wird als Periode bezeichnet. Die Periode der Sinus- und Kosinusfunktion beträgt jeweils <math>2\pi</math>.}} | ||
| − | :* Phasenverschiebung {{versteckt|::Als Phase wird jene Zahl bezeichnet, auf die die Sinus- und die | + | :* Periodendauer <math>\ T</math> {{versteckt|::Die Periodendauer oder Schwingungsdauer gibt die Zeit an, die vergeht während ein schwingungsfähiges System eine Schwingungsperiode durchläuft.}} |
| + | |||
| + | :* Phasenverschiebung {{versteckt|::Als Phase wird jene Zahl bezeichnet, auf die die Sinus- und die Kosinusfunktion angewandt wird. Zwei Funktionen, deren Phasen sich um einen konstanten Wert unterscheiden, beispielsweise <math>x \rightarrow \sin(2x)</math> und <math>x \rightarrow \sin(2x+3)</math> heißen zueinander phasenverschoben. In diesem Beispiel ist die Phasenverschiebung 3.}} | ||
:* Schieberegler {{versteckt|::In den GeoGebra-Applets werden häufig Schieberegler verwendet. Diese werden als Linie mit einem Punkt dargestellt. Der Punkt lässt sich mit gedrückter linker Maustaste bewegen.}} | :* Schieberegler {{versteckt|::In den GeoGebra-Applets werden häufig Schieberegler verwendet. Diese werden als Linie mit einem Punkt dargestellt. Der Punkt lässt sich mit gedrückter linker Maustaste bewegen.}} | ||
| − | :* Schwingungsdauer <math>\ T</math> {{versteckt|::Die Schwingungsdauer gibt die Zeit an, die vergeht während ein schwingungsfähiges System eine Schwingungsperiode durchläuft.}} | + | :* Schwingungsdauer <math>\ T</math> {{versteckt|::Die Schwingungsdauer oder Periodendauer gibt die Zeit an, die vergeht während ein schwingungsfähiges System eine Schwingungsperiode durchläuft.}} |
:* Sinusfunktion {{versteckt|::Die Funktion <math>x \rightarrow \sin (x) </math> mit <math>x\in \R</math> heißt Sinusfunktion.}} | :* Sinusfunktion {{versteckt|::Die Funktion <math>x \rightarrow \sin (x) </math> mit <math>x\in \R</math> heißt Sinusfunktion.}} | ||
| Zeile 54: | Zeile 53: | ||
:* Wellenlänge <math>\ \lambda</math> ("lambda") {{versteckt|::Die Wellenlänge gibt den Abstand zweier Orte im gleichen Schwingungszustand (z.B. Maxima) an. Achtung: Der Abstand zweier benachbarter Nullstellen ist nur die halbe Wellenlänge! }} | :* Wellenlänge <math>\ \lambda</math> ("lambda") {{versteckt|::Die Wellenlänge gibt den Abstand zweier Orte im gleichen Schwingungszustand (z.B. Maxima) an. Achtung: Der Abstand zweier benachbarter Nullstellen ist nur die halbe Wellenlänge! }} | ||
| − | :* Wertemenge | + | :* Wertemenge {{versteckt|::Als Wertemenge bezeichnet man die Menge aller Werte, die eine Funktion annimmt. Beispielsweise besteht die Wertemenge der Sinusfunktion aus allen Werten <math>\ y</math>, die <math>-1 \le y \le 1</math> erfüllen.}} |
| + | |||
| + | :* Winkelgeschwindigkeit <math>\ \omega</math> ("omega") {{versteckt|::Ihre Einheit ist <math>\frac{1}{s}</math>. Es gilt: <math>\omega = 2 \pi f = \frac{2\pi}{T}</math> | ||
| + | ::( <math>\ f</math> Frequenz, <math>\ T</math> Schwingungsdauer)}} | ||
Aktuelle Version vom 3. Juli 2016, 12:12 Uhr
Zum Nachschlagen
- allgemeine Kosinusfunktion [Anzeigen]
- allgemeine Sinusfunktion [Anzeigen]
- allgemeine quadratische Funktion [Anzeigen]
- Amplitude
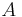 [Anzeigen]
[Anzeigen]
- Amplitude
- Extremum [Anzeigen]
- Frequenz
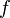 [Anzeigen]
[Anzeigen]
- Frequenz
- Hochpunkt [Anzeigen]
- Kosinusfunktion [Anzeigen]
- Kosinuskurve [Anzeigen]
- Monotonie [Anzeigen]
- Nullstelle [Anzeigen]
- Periode [Anzeigen]
- Periodendauer
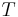 [Anzeigen]
[Anzeigen]
- Periodendauer
- Phasenverschiebung [Anzeigen]
- Schieberegler [Anzeigen]
- Schwingungsdauer
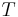 [Anzeigen]
[Anzeigen]
- Schwingungsdauer
- Sinusfunktion [Anzeigen]
- Sinuskurve [Anzeigen]
- Schwingungsperiode [Anzeigen]
- Tiefpunkt [Anzeigen]
- Wellenlänge
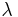 ("lambda") [Anzeigen]
("lambda") [Anzeigen]
- Wellenlänge
- Wertemenge [Anzeigen]
- Winkelgeschwindigkeit
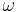 ("omega") [Anzeigen]
("omega") [Anzeigen]
- Winkelgeschwindigkeit
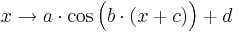 mit
mit 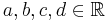 und
und 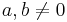
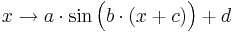 mit
mit 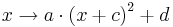 mit
mit 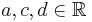 und
und 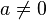
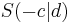
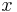 , an der
, an der 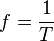
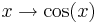 mit
mit 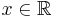 heißt Kosinusfunktion.
heißt Kosinusfunktion.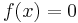 gilt.
gilt.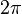 .
.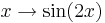 und
und 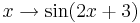 heißen zueinander phasenverschoben. In diesem Beispiel ist die Phasenverschiebung 3.
heißen zueinander phasenverschoben. In diesem Beispiel ist die Phasenverschiebung 3.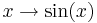 mit
mit 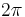 .
.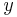 , die
, die 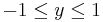 erfüllen.
erfüllen. . Es gilt:
. Es gilt: