Zum Nachschlagen: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
K (→Zum Nachschlagen) |
(Navigation) |
||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Trigonometrische Funktionen}} | |
| − | + | ||
| − | + | ||
| Zeile 22: | Zeile 20: | ||
:* Frequenz <math>\ f</math> {{versteckt|::Als Frequenz <math>\ f</math> bezeichnet man die Anzahl der durchlaufenen Schwingungsperioden pro Zeitintervall. Ihre Einheit ist Hertz (abgekürzt Hz). Werden beispielsweise 50 Schwingungsperioden pro Sekunde durchlaufen, so sagt man, die Schwingung hat 50 Hz. | :* Frequenz <math>\ f</math> {{versteckt|::Als Frequenz <math>\ f</math> bezeichnet man die Anzahl der durchlaufenen Schwingungsperioden pro Zeitintervall. Ihre Einheit ist Hertz (abgekürzt Hz). Werden beispielsweise 50 Schwingungsperioden pro Sekunde durchlaufen, so sagt man, die Schwingung hat 50 Hz. | ||
| − | ::Es gilt: <math>f = \frac{1}{T}</math>}} | + | ::Es gilt: <math>f = \frac{1}{T}</math> |
| + | ::( <math>\ T </math> Schwingungsdauer)}} | ||
:* Hochpunkt {{versteckt|::Ein Hochpunkt einer Funktion <math>\ f</math> ist eine Stelle <math>\ x</math>, an der <math>\ f</math> größere Werte besitzt als an allen anderen Stellen einer kleinen Umgebung von <math>\ x</math>.}} | :* Hochpunkt {{versteckt|::Ein Hochpunkt einer Funktion <math>\ f</math> ist eine Stelle <math>\ x</math>, an der <math>\ f</math> größere Werte besitzt als an allen anderen Stellen einer kleinen Umgebung von <math>\ x</math>.}} | ||
| Zeile 36: | Zeile 35: | ||
:* Periode {{versteckt|::Der Abstand zweier Orte im gleichen Schwingungszustand wird als Periode bezeichnet. Die Periode der Sinus- und Kosinusfunktion beträgt jeweils <math>2\pi</math>.}} | :* Periode {{versteckt|::Der Abstand zweier Orte im gleichen Schwingungszustand wird als Periode bezeichnet. Die Periode der Sinus- und Kosinusfunktion beträgt jeweils <math>2\pi</math>.}} | ||
| − | :* Phasenverschiebung {{versteckt|::Als Phase wird jene Zahl bezeichnet, auf die die Sinus- und die | + | :* Periodendauer <math>\ T</math> {{versteckt|::Die Periodendauer oder Schwingungsdauer gibt die Zeit an, die vergeht während ein schwingungsfähiges System eine Schwingungsperiode durchläuft.}} |
| + | |||
| + | :* Phasenverschiebung {{versteckt|::Als Phase wird jene Zahl bezeichnet, auf die die Sinus- und die Kosinusfunktion angewandt wird. Zwei Funktionen, deren Phasen sich um einen konstanten Wert unterscheiden, beispielsweise <math>x \rightarrow \sin(2x)</math> und <math>x \rightarrow \sin(2x+3)</math> heißen zueinander phasenverschoben. In diesem Beispiel ist die Phasenverschiebung 3.}} | ||
:* Schieberegler {{versteckt|::In den GeoGebra-Applets werden häufig Schieberegler verwendet. Diese werden als Linie mit einem Punkt dargestellt. Der Punkt lässt sich mit gedrückter linker Maustaste bewegen.}} | :* Schieberegler {{versteckt|::In den GeoGebra-Applets werden häufig Schieberegler verwendet. Diese werden als Linie mit einem Punkt dargestellt. Der Punkt lässt sich mit gedrückter linker Maustaste bewegen.}} | ||
| − | :* Schwingungsdauer <math>\ T</math> {{versteckt|::Die Schwingungsdauer gibt die Zeit an, die vergeht während ein schwingungsfähiges System eine Schwingungsperiode durchläuft.}} | + | :* Schwingungsdauer <math>\ T</math> {{versteckt|::Die Schwingungsdauer oder Periodendauer gibt die Zeit an, die vergeht während ein schwingungsfähiges System eine Schwingungsperiode durchläuft.}} |
:* Sinusfunktion {{versteckt|::Die Funktion <math>x \rightarrow \sin (x) </math> mit <math>x\in \R</math> heißt Sinusfunktion.}} | :* Sinusfunktion {{versteckt|::Die Funktion <math>x \rightarrow \sin (x) </math> mit <math>x\in \R</math> heißt Sinusfunktion.}} | ||
| Zeile 52: | Zeile 53: | ||
:* Wellenlänge <math>\ \lambda</math> ("lambda") {{versteckt|::Die Wellenlänge gibt den Abstand zweier Orte im gleichen Schwingungszustand (z.B. Maxima) an. Achtung: Der Abstand zweier benachbarter Nullstellen ist nur die halbe Wellenlänge! }} | :* Wellenlänge <math>\ \lambda</math> ("lambda") {{versteckt|::Die Wellenlänge gibt den Abstand zweier Orte im gleichen Schwingungszustand (z.B. Maxima) an. Achtung: Der Abstand zweier benachbarter Nullstellen ist nur die halbe Wellenlänge! }} | ||
| − | :* Wertemenge {{versteckt|::Als Wertemenge bezeichnet man die Menge aller Werte, die eine Funktion | + | :* Wertemenge {{versteckt|::Als Wertemenge bezeichnet man die Menge aller Werte, die eine Funktion annimmt. Beispielsweise besteht die Wertemenge der Sinusfunktion aus allen Werten <math>\ y</math>, die <math>-1 \le y \le 1</math> erfüllen.}} |
| − | :* Winkelgeschwindigkeit <math>\ \omega</math> ("omega") {{versteckt|::Es gilt: <math>\omega = 2 \pi f = \frac{2\pi}{T}</math>}} | + | :* Winkelgeschwindigkeit <math>\ \omega</math> ("omega") {{versteckt|::Ihre Einheit ist <math>\frac{1}{s}</math>. Es gilt: <math>\omega = 2 \pi f = \frac{2\pi}{T}</math> |
| + | ::( <math>\ f</math> Frequenz, <math>\ T</math> Schwingungsdauer)}} | ||
Aktuelle Version vom 3. Juli 2016, 12:12 Uhr
Zum Nachschlagen
- allgemeine Kosinusfunktion [Anzeigen]
- allgemeine Sinusfunktion [Anzeigen]
- allgemeine quadratische Funktion [Anzeigen]
- Amplitude
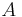 [Anzeigen]
[Anzeigen]
- Amplitude
- Extremum [Anzeigen]
- Frequenz
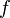 [Anzeigen]
[Anzeigen]
- Frequenz
- Hochpunkt [Anzeigen]
- Kosinusfunktion [Anzeigen]
- Kosinuskurve [Anzeigen]
- Monotonie [Anzeigen]
- Nullstelle [Anzeigen]
- Periode [Anzeigen]
- Periodendauer
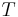 [Anzeigen]
[Anzeigen]
- Periodendauer
- Phasenverschiebung [Anzeigen]
- Schieberegler [Anzeigen]
- Schwingungsdauer
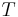 [Anzeigen]
[Anzeigen]
- Schwingungsdauer
- Sinusfunktion [Anzeigen]
- Sinuskurve [Anzeigen]
- Schwingungsperiode [Anzeigen]
- Tiefpunkt [Anzeigen]
- Wellenlänge
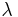 ("lambda") [Anzeigen]
("lambda") [Anzeigen]
- Wellenlänge
- Wertemenge [Anzeigen]
- Winkelgeschwindigkeit
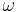 ("omega") [Anzeigen]
("omega") [Anzeigen]
- Winkelgeschwindigkeit
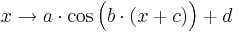 mit
mit 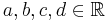 und
und 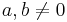
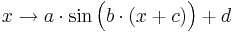 mit
mit 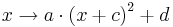 mit
mit 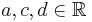 und
und 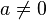
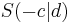
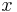 , an der
, an der 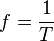
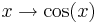 mit
mit 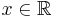 heißt Kosinusfunktion.
heißt Kosinusfunktion.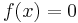 gilt.
gilt.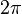 .
.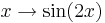 und
und 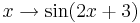 heißen zueinander phasenverschoben. In diesem Beispiel ist die Phasenverschiebung 3.
heißen zueinander phasenverschoben. In diesem Beispiel ist die Phasenverschiebung 3.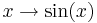 mit
mit 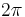 .
.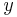 , die
, die 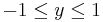 erfüllen.
erfüllen. . Es gilt:
. Es gilt: