Potenzfunktionen - 2. Stufe: Unterschied zwischen den Versionen
| (66 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Potenzfunktionen}} | |
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | < | + | == Die Graphen der Funktionen f(x) = x<sup>-n</sup>, n <small>∈</small> IN == |
| + | === Gerade Potenzen === | ||
| + | '''Wir betrachten zunächst die Graphen der Funktionen f(x) = x<sup>-n</sup>, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...''' | ||
| − | <ggb_applet height=" | + | {| cellspacing="10" |
| − | filename=" | + | |- style="vertical-align:top;" |
| + | | {{Arbeiten|NUMMER=1|ARBEIT= | ||
| + | # Mit dem Schieberegler kannst du den Exponenten verändern. Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf | ||
| + | #* Symmetrie | ||
| + | #* Monotonie | ||
| + | #* größte und kleinste Funktionswerte | ||
| + | # Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. <br> <pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen </pre> | ||
| + | # Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x<sup>-2</sup> zu f(x) = x<sup>-4</sup>, dann die beim Übergang von f(x) = x<sup>-4</sup> zu f(x) = x<sup>-6</sup> usw.! | ||
| + | # Wie ändern sich die y-Werte bei f(x) = x<sup>-n</sup>, n gerade, wenn der x-Wert ver-k-facht wird? | ||
| + | :{{Lösung versteckt| | ||
| + | : zu 1.) | ||
| + | :* Alle Graphen sind Achsensymmetrisch zur y-Achse | ||
| + | :* Für die betrachteten Exponenten sind alle Graphen im Intervall <math>]-\infty;0[</math> streng monoton steigend und im Intervall <math>]0;\infty[</math> streng monoton fallend. | ||
| + | :* Die Funktionswerte aller Graphen sind positiv, ihre Wertebereiche sind <math>]0; \infty[</math>. Die x-Achse und die y-Achse sind Asympthoden der Funktionsgraphen. | ||
| + | :<br /> | ||
| + | : zu 2.) Unabhängig vom Exponenten n laufen allge Graphen durch die Punkte (-1;1) und (1;1). | ||
| + | :: '''Begründung''' für den Punkt (-1;1): An der Stelle x<math>=</math>-1 ist <math>f(x)=f(-1)=(-1)^{-n}=\textstyle \frac{1}{(-1)^n}.</math> Da wir hier nur gerade Zahlen <math>n \in \{2,4,6,...\}</math> betrachten gilt weiter: <math>\textstyle \frac{1}{(-1)^n}= \textstyle \frac{1}{1}=1</math> unabhängig von n. | ||
| + | :: '''Begründung''' für den Punkt (1;1): An der Stelle x<math>=</math>1 ist <math>f(x)=f(1)=1^{-n}=\textstyle \frac{1}{1^n}=1</math> für alle <math>n \in {\Bbb N}.</math> | ||
| + | :<br /> | ||
| + | :zu 3.) Die Punkte (-1;1) und (1;1) bleiben unverändert. | ||
| + | :: Dazwischen, genauer in den Intervallen ]-1;0[ und ]0;1[ werden die Fuktionswerte kleiner, an den Stellen x für x < -1 bzw. x > 1 werden die Funktionswerte größer. | ||
| + | :<br /> | ||
| + | : zu 4.) | ||
| + | : Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-<math>\textstyle \frac{1}{k^n}</math>-facht. <br> | ||
| + | :: Symbolisch: <math>f(k \cdot x) = (k\cdot x)^{-n} = k^{-n} \cdot x^{-n} =\textstyle \frac {1}{k^n} \cdot f(x)</math>. | ||
| + | }} | ||
| + | }}<br> | ||
| + | || <ggb_applet height="300" width="350" showMenuBar="false" showResetIcon="true" | ||
| + | filename="3_gerade_x_minus_n.ggb" /> | ||
| + | |} | ||
| + | |||
| + | === Parabel und Hyperbel === | ||
| + | |||
| + | Du hast nun Potenzfunktionen der Form f(x)=x<sup>n</sup> und f(x)=x<sup>-n</sup> kennengelernt. Ihre Graphen spielen in der Mathematik und in den Naturwissenschaften eine wichtige Rolle. Sie haben deshalb eigene Bezeichnungen: | ||
| + | {{ Merksatz | MERK = | ||
| + | * Die Graphen von Funktionen f(x)=x<sup>n</sup> und einer natürlichen Zahl n heißen '''Parabeln''', oder genauer: '''Parabel ''n''-ter Ordnung'''. <BR> | ||
| + | * Für f(x)=x<sup>2</sup> heißt der Graph '''Normalparabel'''; für f(x)=x<sup>3</sup> dann nennt man den Graphen '''kubische Grundparabel''' (oder '''Parabel dritter Ordnung'''). | ||
| + | * Die Graphen von Funktionen f(x)=x<sup>-n</sup> und einer natürlichen Zahl n heißen '''Hyperbeln (n-ter Ordnung)'''. Diese haben die x- und die y-Achse als Asymptoten. | ||
| + | }} | ||
| + | <br /> | ||
| + | |||
| + | === Ungerade Potenzen === | ||
| + | |||
| + | '''Wir betrachten nun die Graphen der Funktionen f(x) = x<sup>-n</sup>, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..''' | ||
| + | |||
| + | {| <!--class="prettytable sortable" --> | ||
| + | |- style="vertical-align:top;" | ||
| + | | <ggb_applet height="300" width="350" showMenuBar="false" showResetIcon="true" | ||
| + | filename="3_ungerade_x_minus_n.ggb" /> | ||
| + | || | ||
| + | {{Arbeiten|NUMMER=2|ARBEIT= | ||
| + | # Beschreibe wieder die Graphen! Achte dabei auf | ||
| + | #* Symmetrie | ||
| + | #* Monotonie | ||
| + | #* größte und kleinste Funktionswerte | ||
| + | # Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe!<br><pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen</pre> | ||
| + | # Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x<sup>-1</sup> zu f(x) = x<sup>-3</sup>, dann die beim Übergang von f(x) = x<sup>-3</sup> zu f(x) = x<sup>-5</sup> usw.! | ||
| + | {{ Lösung versteckt | | ||
| + | zu 1.) | ||
| + | :* Die Graphen sind punktsymmetrisch zum Ursprung (0;0). | ||
| + | :: Beachte: für n<math>=</math>1 ist der Graph zusätzlich achsensymmetrisch zur Geraden g: y<math>=</math>x. | ||
| + | :* Alle Graphen sind auf ihrem Definitionsbereich <math>\scriptstyle {\Bbb D} = {\Bbb R}\backslash \{0\}</math> streng monoton fallend. | ||
| + | :* Als Funktionswerte werden alle Werte aus <math>\scriptstyle {\Bbb R}\backslash \{0\}</math>. Damit sind Definitionsbereich und Wertebereich gleich. | ||
| + | <br /> | ||
| + | zu 2.) Alle Graphen verlaufen durch die Punkte (-1;-1) und (1;1). | ||
| + | : '''Begründung''' für Punkt (-1;-1): An der Stelle x<math>=</math>-1 ist <math>f(x)=f(-1)=(-1)^{-n}=\textstyle \frac{1}{(-1)^n}=\textstyle \left( \frac{\,\,1}{-1}\right)^n</math>. Da die Zahl n nach Voraussetzung ungerade ist, ist (n-1) eine gerade Zahl. Deswegen ist <math>\textstyle \left( \frac{\,\,1}{-1}\right)^n =\left( \frac{\,\,1}{-1}\right) \cdot \left( \frac{\,\,1}{-1}\right)^{n-1}=\left( \frac{\,\,1}{-1}\right) \cdot \left( \frac{1}{1}\right)^{n-1} = -1</math> für alle betrachteten n. | ||
| + | : '''Begründung''' für den Punkt (1;1): An der Stelle x<math>=</math>1 ist <math>f(x)=f(1)=1^{-n}=\textstyle \frac{1}{1^n}=1</math> für alle <math>n \in {\Bbb N}.</math> | ||
| + | zu 3.) Die Punkte (-1;-1) und (1;1) bleiben von der Änderung unberührt. | ||
| + | : In den Intervallen ]-∞;-1[ und ]1;∞[ schmiegt sich der Graph näher an die y-Achse an, wenn n erhöht wird. | ||
| + | : In den Intervallen ]-1;0[ un ]0;1[ werden die Graphen steiler, wenn n erhöht wird. | ||
| + | }} | ||
| + | }} | ||
| + | |} | ||
| + | |||
| + | === Teste dein Wissen === | ||
| + | {{Arbeiten|NUMMER=3|ARBEIT= | ||
| + | Wir betrachten die Funktionen der Form f(x) = x<sup>-n</sup>, n eine natürliche Zahl | ||
| + | # Für welches n verläuft der Graph durch den Punkt <math>P(2;\textstyle \frac{1}{16})</math>? | ||
| + | # Für welches n verläuft der Graph durch <math>Q ( 0,\!5;8 )</math>? | ||
| + | :{{Lösung versteckt| | ||
| + | zu 1.) Die Lösung ist n<math>=</math>4. | ||
| + | : '''Begründung:''' Es gilt <math>f(2) = \textstyle \frac{1}{2^4} = \frac 1{16}.</math> | ||
| + | zu 2.) Die Lösung ist n<math>=</math>3. | ||
| + | : '''Begründung:''' Es gilt <math>f(0,\!5) = \textstyle \frac{1}{(0,5)^3} = 2^3 = 8</math> | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | == Die Graphen von f(x) = a x<sup>-n</sup> mit a <small>∈</small> IR == | ||
| + | |||
| + | '''Wir betrachten jetzt die Funktionen der Form <math>f(x) = a \cdot x^{-n} </math>, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n <small>∈</small> IN, a <small>∈</small> IR .''' | ||
| + | |||
| + | {| <!--class="prettytable sortable"--> | ||
| + | |- style="vertical-align:top;" | ||
| + | | {{Arbeiten|NUMMER=4|ARBEIT= | ||
| + | # Es sei zunächst n = 2, also <math>f(x) = a \cdot x^{-2}</math>. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a! | ||
| + | # Beschreibe die Veränderung der Graphen von <math>f(x) = a \cdot x^{-n} </math> bei der Veränderung des Parameter a! Unterscheide dabei wieder zwischen geraden und ungeraden Exponenten. | ||
| + | {{ Lösung versteckt | | ||
| + | : zu 1.) | ||
| + | :* Für 1 < a wird der Graph der Funktion gestreckt und wird für 0<a<1 gestaucht. | ||
| + | :* Für a<math>=</math>1 bleibt er unverändert | ||
| + | :* Für a<math>=</math>0 wird die Funktion zur ''Nullfunktion'' f(x)<math>=</math>0 für alle x. | ||
| + | :* Der Wert a<math>=</math>-1 bewirkt eine Spiegelung des Graphen an der x-Achse; alle übrigen Fälle ergeben sich daraus. | ||
| + | : zu 2.) | ||
| + | :: Die Beobachtungen aus 1.) übertragen sich auch für beliebige Exponenten. | ||
| + | }} | ||
| + | }} | ||
| + | || <ggb_applet height="300" width="350" showMenuBar="false" showResetIcon="true" | ||
| + | filename="4_ax_minus_n.ggb" /> | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | {| <!--class="prettytable sortable"--> | ||
| + | |- style="vertical-align:top;" | ||
| + | | <ggb_applet height="350" width="450" showMenuBar="false" showResetIcon="true" | ||
| + | filename="4_ax_minus_n_test.ggb" /> | ||
| + | || | ||
| + | {{Arbeiten|NUMMER=5|ARBEIT= | ||
| + | Wir betrachten wieder die Funktionen <math>f(x) = a \cdot x^{-n}</math> für eine eine natürliche Zahl n. | ||
| + | # Bestimme a und n so, dass der Graph durch die Punkte '''A(-1;-2)''' und '''B(2;1)''' verläuft.<br /> Die nebenstehende Graphik dient als Hilfe; die Punkte A und B kannst du darin frei verschieben. | ||
| + | # Bestimme a und n so, dass der Graph durch die Punkte '''A(-1;-1)''' und '''B(1;3)''' verläuft. Was fällt auf? Erkläre deine Beobachtungen. | ||
| + | :{{Lösung versteckt| | ||
| + | : zu 1.) Die Lösung ist a<math>=</math>2, n<math>=</math>1. | ||
| + | :: '''Begründung:''' <math>f(-1)=2\cdot (-1)^{-1} = -2</math> und <math>f(2)=2\cdot (2)^{-1} = 1.</math> | ||
| + | : zu 2.) Es gibt KEINE Lösung. | ||
| + | : '''Begründung:''' | ||
| + | :* Da die y-Komponente des Punktes A(-1;-1) negativ ist, die des Punktes B(1;3) dagegen positiv, muss die gesuchte Zahl n ungerade sein. | ||
| + | :* Wenn der Graph der gesuchten Funktion durch den Punkt A(-1;-1) laufen soll, muss der Parameter a<math>=</math>1 sein. | ||
| + | : Zusammengenommen ist die gesuchte Funktion von der Art f(x)<math>=</math> x<sup>-n</sup> mit ungeradem n. Diese Funktionen haben alle an der Stelle x<math>=</math>1 den Funktionswert f(x)<math>=</math>1. Daher kann es keine Funktion geben, die an der Stelle x<math>=</math>1 den Funktionswert f(x)<math>=</math>3 hat. | ||
| + | }} | ||
| + | }} | ||
| + | |} | ||
| + | |||
| + | === Teste Dein Wissen === | ||
| + | |||
| + | * [http://www.realmath.de/Neues/Klasse10/potenzfunktion/defpotquiz.html Ordne dem Graphen der Potenzfunktion die richtige Gleichung zu!] | ||
| + | * [http://www.tiburski.de/cybernautenshop/virtuelle_schule/dfu/potenzfunktionen/potenzfunktionen_II.html Erkenne die Art der Funktion und ordne dem Graphen die entsprechende Funktionsgleichung zu!] | ||
| + | <br /><br /> | ||
| + | |||
| + | ---- | ||
| + | {|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="120"|[[Bild:Maehnrot.jpg|100px]] | ||
| + | |align = "left"|'''Als nächstes erfährst du etwas über Potenzfunktionen, die Stammbrüche im Exponenten haben.'''<br /> | ||
| + | [[Bild:Pfeil.gif]] [[Potenzfunktionen_3._Stufe|'''Hier geht es weiter''']]'''.''' | ||
| + | |||
| + | |} | ||
Aktuelle Version vom 17. Januar 2011, 11:09 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen f(x) = x-n, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen f(x) = x-n, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
|
Parabel und Hyperbel
Du hast nun Potenzfunktionen der Form f(x)=xn und f(x)=x-n kennengelernt. Ihre Graphen spielen in der Mathematik und in den Naturwissenschaften eine wichtige Rolle. Sie haben deshalb eigene Bezeichnungen:
|
Merke:
|
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen f(x) = x-n, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
Teste dein Wissen
|
Wir betrachten die Funktionen der Form f(x) = x-n, n eine natürliche Zahl
zu 1.) Die Lösung ist n
zu 2.) Die Lösung ist n
|
Die Graphen von f(x) = a x-n mit a ∈ IR
Wir betrachten jetzt die Funktionen der Form 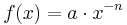 , wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
|
|
Teste Dein Wissen
- Ordne dem Graphen der Potenzfunktion die richtige Gleichung zu!
- Erkenne die Art der Funktion und ordne dem Graphen die entsprechende Funktionsgleichung zu!

|
Als nächstes erfährst du etwas über Potenzfunktionen, die Stammbrüche im Exponenten haben. |
![]-\infty;0[](/images/math/b/5/0/b506be48eafe7c01cce18da0d9f808f4.png) streng monoton steigend und im Intervall
streng monoton steigend und im Intervall ![]0;\infty[](/images/math/d/c/f/dcfb1c7331a6972af80f5df85fdfb44d.png) streng monoton fallend.
streng monoton fallend.
 -1 ist
-1 ist 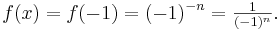 Da wir hier nur gerade Zahlen
Da wir hier nur gerade Zahlen 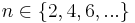 betrachten gilt weiter:
betrachten gilt weiter: 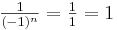 unabhängig von n.
unabhängig von n.
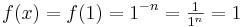 für alle
für alle 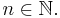
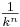 -facht.
-facht. 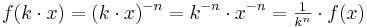 .
.
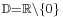 streng monoton fallend.
streng monoton fallend.
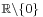 . Damit sind Definitionsbereich und Wertebereich gleich.
. Damit sind Definitionsbereich und Wertebereich gleich.
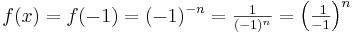 . Da die Zahl n nach Voraussetzung ungerade ist, ist (n-1) eine gerade Zahl. Deswegen ist
. Da die Zahl n nach Voraussetzung ungerade ist, ist (n-1) eine gerade Zahl. Deswegen ist 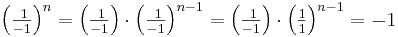 für alle betrachteten n.
für alle betrachteten n.
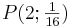 ?
?
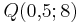 ?
?
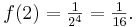
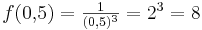
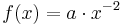 . Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
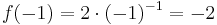 und
und