Bestimmung der Funktionsgleichung aus dem Graphen: Unterschied zwischen den Versionen
K |
(Navigation) |
||
| (67 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Trigonometrische Funktionen}} | |
| − | [[Trigonometrische_Funktionen | + | |
| − | </ | + | ===FAQ=== |
| + | [[Trigonometrische_Funktionen/Zum_Nachschlagen|Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | <span style="background-color:yellow;">Hefteintrag:</span> Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben! | ||
===Informationen aus dem Graphen=== | ===Informationen aus dem Graphen=== | ||
{| | {| | ||
| − | |<ggb_applet height="260" width="330" filename="InfoausdemGraphen_3.ggb" /> <br> | + | | |
| + | [[bild:InfoausdemGraphen_3.png|300px]] | ||
| + | <!--<ggb_applet height="260" width="330" filename="InfoausdemGraphen_3.ggb" /> <br> --> | ||
|| | || | ||
{{Arbeiten|NUMMER=1|ARBEIT= | {{Arbeiten|NUMMER=1|ARBEIT= | ||
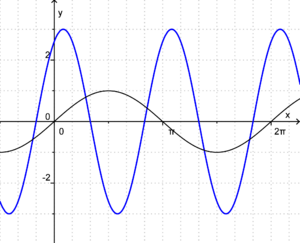
Auf diesem Bild ist ein Graph einer allgemeinen Sinusfunktion (blau) zu sehen. Von diesem sollen nun einige Eigenschaften bestimmt werden. Als Hilfe wurde zusätzlich die Sinuskurve eingezeichnet. <br> | Auf diesem Bild ist ein Graph einer allgemeinen Sinusfunktion (blau) zu sehen. Von diesem sollen nun einige Eigenschaften bestimmt werden. Als Hilfe wurde zusätzlich die Sinuskurve eingezeichnet. <br> | ||
# Gib die Amplitude des Graphen an! | # Gib die Amplitude des Graphen an! | ||
| − | # Gib die Wertemenge an | + | # Gib die Wertemenge an! |
# Bestimme die Periode! | # Bestimme die Periode! | ||
| − | # Gib die Nullstellen der Funktion an | + | # Gib die Nullstellen der Funktion an!<br> |
# An welchen Stellen sind die Funktionswerte am kleinsten und wo sind sie am größten? <br> | # An welchen Stellen sind die Funktionswerte am kleinsten und wo sind sie am größten? <br> | ||
| − | # Nenne jeweils einen Bereich in dem der Graph streng monoton fallend bzw. steigend ist | + | # Nenne jeweils einen Bereich in dem der Graph streng monoton fallend bzw. steigend ist! |
}} | }} | ||
| + | ||{{#ev:youtube|tgd8W2X01P4|150}} | ||
|} | |} | ||
===Bestimmung einer Funktionsgleichung aus dem Graphen=== | ===Bestimmung einer Funktionsgleichung aus dem Graphen=== | ||
| − | Beachte, zu einem Graphen kann es mehrere zugehörige Funktionsgleichungen geben | + | {| |
| + | | | ||
| + | {{Merksatz|MERK= | ||
| + | Beachte, zu einem Graphen kann es mehrere zugehörige Funktionsgleichungen geben! D.h., die Antwort auf die Frage nach einer Funktionsgleichung zu einem gegebenen Graphen muss nicht immer eindeutig sein. | ||
| + | Um zu sehen wie man aus dem Graphen einer Funktion eine zugehörige Funktionsgleichung bestimmen kann, klicke [[Trigonometrische_Funktionen/Bestimmung_der_Funktionsgleichung|hier]].}} | ||
| + | ||{{#ev:youtube|SH3FtIqopMY|150}} | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| | ||
| + | | | ||
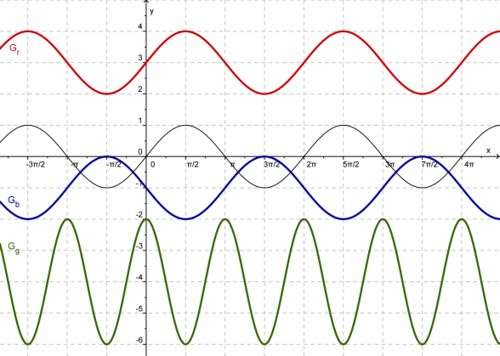
{{Arbeiten|NUMMER=2|ARBEIT= | {{Arbeiten|NUMMER=2|ARBEIT= | ||
| − | + | Bestimme zu folgenden Graphen je einen zugehörigen Funktionsterm der Form <math> x\rightarrow a\cdot\sin\Big(b\cdot (x+c)\Big)+d </math>. | |
}} | }} | ||
| − | + | ||{{#ev:youtube|Sazk7iSdwF8|150}} | |
| + | |} | ||
| − | + | :[[bild:Kontrolle_5.jpg|500px]] | |
| − | + | ||
| − | + | ||
| − | <ggb_applet height="460" width="635" filename=" | + | <!-- <ggb_applet height="460" width="635" filename="Kontrolle_5.ggb" /> <br> --> |
---- | ---- | ||
| Zeile 38: | Zeile 55: | ||
'''Jetzt noch was zum Knobeln!!!''' | '''Jetzt noch was zum Knobeln!!!''' | ||
| − | {{Arbeiten|NUMMER= | + | {| |
| − | # In diesem [http://www.mathe-online.at/mathint/fun2/applet_b_grapherk3.html Applet] kannst zu zeigen, ob du zu | + | | |
| − | # Gib einen Funktionsterm zu dem Graphen an, den man erhält falls die Sinuskurve um zwei nach links und um 3 nach oben verschoben wird! Wie lautet die Gleichung, falls zusätzlich die Periode halbiert werden soll?}} | + | {{Arbeiten|NUMMER=3|ARBEIT= |
| + | # In diesem <!-- [http://www.mathe-online.at/mathint/fun2/applet_b_grapherk3.html Applet]--> [http://www.mathe-online.at/galerie/fun2/fun2.html#grapherk3 Applet] (Bitte klicke dann auf '''Graphen erkennen 3'''!) <!-- und in diesem [[Trigonometrische_Funktionen/Bestimmung_der_Funktionsgleichung_aus_dem_Graphen/Applet|Applet]] -->kannst zu zeigen, ob du zu den gegebenen Graphen den zugehörigen Term findest. | ||
| + | # Gib einen Funktionsterm zu dem Graphen an, den man erhält, falls die Sinuskurve um zwei nach links und um 3 nach oben verschoben wird! Wie lautet die Gleichung, falls zusätzlich die Periode halbiert werden soll?}} | ||
| + | ||{{#ev:youtube|HkvPXgsQ4Ok|150}} | ||
| + | |} | ||
---- | ---- | ||
| − | '' | + | '''Anwendungsbeispiel - Erdbeben''' |
| − | + | {| border=0 | |
| + | |[[bild:Abb1.gif|center|200px]] | ||
| + | |rowspan=2 | {{Arbeiten|NUMMER=4|ARBEIT= | ||
| + | Die Abbildung zeigt dir, wie man die Bewegung eines schwingenden Objekts mit Hilfe eines Streifen Papier, der an ihm mit konstanter Geschwindigkeit vorbei gezogen wird, "festhalten kann". | ||
| + | Auf diese Weise kann die Auslenkung als Funktion der Zeit aufgezeichnet werden. Nach diesem Prinzip können beispielsweise die Schwingungen, die ein Erdbeben auslöst, protokolliert werden. | ||
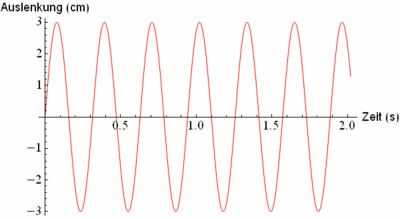
| + | Die folgende Abbildung zeigt ein solches "Protokoll". | ||
| + | * Wie viele Einzelschwingungen führt das Objekt pro Sekunde aus? [[Trigonometrische_Funktionen/Anwendungen_in_der_Physik/Tipp|Tipp!]] | ||
| + | * Stelle die Funktionsgleichung der Schwingung auf! | ||
| + | :[[bild:Abb2.gif|left|400px]] | ||
| + | }} | ||
| + | ||{{#ev:youtube|KrmzJeHgcAY|150}} | ||
| + | |} | ||
| − | + | ---- | |
| − | + | {| | |
| + | | | ||
| + | Super! Nun hast du es geschafft und das Ende der zweiten Station erreicht. | ||
| − | + | <span style="background-color:yellow;">Hefteintrag:</span> Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alles Wichtige notiert hast! | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | Falls du noch etwas üben möchtest, so löse die Zusatzaufgabe! | ||
| + | ||{{#ev:youtube|t2GqsU-oQfw|150}} | ||
| + | |} | ||
| + | ---- | ||
| + | {| | ||
| + | | | ||
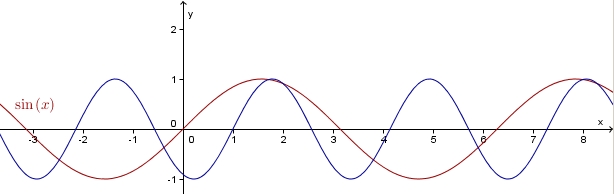
| + | {{Arbeiten|NUMMER=5 - Zusatzaufgabe|ARBEIT= | ||
| + | In dem unteren Bild sind die Sinuskurve (rot) und ein Graph einer allgemeinen Sinusfunktion (schwarz) zu sehen.<br> | ||
| + | # Du kennst die Nullstellen der Sinusfunktion. Wo sind sie?<br> | ||
| + | # Stelle in der Zeichnung fest, an welchen Stellen der schwarze Graph Nullstellen besitzt und notiere sie!<br> | ||
| + | # Wo hat der Graph der schwarzen Funktion Hochpunkte bzw. Tiefpunkte?<br> | ||
| + | # Wo ist er streng monoton fallend bzw. steigend? | ||
}} | }} | ||
| + | ||{{#ev:youtube|uNRxqbtKXOU|150}} | ||
| + | |} | ||
| + | <!-- [[bild:sin(2x-2).jpg|center]] --> | ||
| + | :[[bild:sin(2x-2).jpg]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
| − | + | [[Trigonometrische_Funktionen/Bestimmung_der_Funktionsgleichung_aus_dem_Graphen/Lösung_zu_Aufgabe_1|Lösung zu Aufgabe 1]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | [[Trigonometrische Funktionen/Bestimmung der Funktionsgleichung aus dem Graphen/Aufgabe3|Lösung zu Aufgabe 2]] | |
| − | + | [[Trigonometrische_Funktionen/Bestimmung_der_Funktionsgleichung_aus_dem_Graphen/Lösung_zu_Aufgabe_3|Lösung zu Aufgabe 3]] | |
| − | + | [[Trigonometrische_Funktionen/Bestimmung_der_Funktionsgleichung_aus_dem_Graphen/Lösung_zu_Aufgabe_4|Lösung zu Aufgabe 4]] | |
| − | + | ||
| + | [[Trigonometrische_Funktionen/Bestimmung_der_Funktionsgleichung_aus_dem_Graphen/Lösung_zu_Aufgabe_5|Lösung zu Aufgabe 5]] | ||
---- | ---- | ||
Aktuelle Version vom 3. Juli 2016, 11:04 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Hefteintrag: Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben!
Informationen aus dem Graphen
|
Bestimmung einer Funktionsgleichung aus dem Graphen
|
|
Jetzt noch was zum Knobeln!!!
|
Anwendungsbeispiel - Erdbeben
|
|
Super! Nun hast du es geschafft und das Ende der zweiten Station erreicht. Hefteintrag: Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alles Wichtige notiert hast! Falls du noch etwas üben möchtest, so löse die Zusatzaufgabe! |
|
Weiter geht es mit

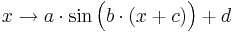 .
.