Einfluss von c: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(→Einfluss von c: Vorlage Video eingefügt) |
(→Einfluss von c: Video aktualisiert) |
||
| (12 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
# Überlege dir, wie sich die Werte <math> \ c = 2 </math> und <math> \ c = -1 </math>, sowie <math> \ c = 0,5 </math> und <math> \ c = \frac{\pi}{2} </math> auf den Graphen auswirken und überprüfe deine Vermutung. <br> | # Überlege dir, wie sich die Werte <math> \ c = 2 </math> und <math> \ c = -1 </math>, sowie <math> \ c = 0,5 </math> und <math> \ c = \frac{\pi}{2} </math> auf den Graphen auswirken und überprüfe deine Vermutung. <br> | ||
# Formuliere das Ergebnis deiner Untersuchungen. <br> | # Formuliere das Ergebnis deiner Untersuchungen. <br> | ||
| − | |||
}} | }} | ||
| − | ||{{#ev:youtube| | + | ||{{#ev:youtube|ZcCiCyKtuis|150}} |
| + | |} | ||
| + | |||
| + | |||
| + | {| | ||
| + | | | ||
| + | {{Arbeiten|NUMMER=C2|ARBEIT= | ||
| + | |||
| + | Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen! | ||
| + | }} | ||
| + | ||{{#ev:youtube|_gcwpOotsNA|150}} | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| | ||
| + | | | ||
| + | {{Arbeiten|NUMMER=C3|ARBEIT= | ||
| + | |||
| + | Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! | ||
| + | }} | ||
| + | ||{{#ev:youtube|r7sg9UQsU9A|150}} | ||
|} | |} | ||
| Zeile 49: | Zeile 68: | ||
:<math> x \rightarrow \cos ( x + c ) </math>. | :<math> x \rightarrow \cos ( x + c ) </math>. | ||
| − | {{Arbeiten|NUMMER= | + | {{Arbeiten|NUMMER=C4|ARBEIT= |
<ggb_applet height="50" width="150" type="button" filename="cos_c.ggb" /> <br> | <ggb_applet height="50" width="150" type="button" filename="cos_c.ggb" /> <br> | ||
| − | Öffne dieses GeoGebra-Applet und bearbeite damit | + | Öffne dieses GeoGebra-Applet und bearbeite damit die Aufgaben C1/ 2-4 noch einmal. |
}} | }} | ||
| − | ||{{#ev:youtube| | + | ||{{#ev:youtube|VfLQbhcoqKs|150}} |
|} | |} | ||
---- | ---- | ||
| − | |||
| − | + | [[Einfluss_von_c/Lösung_zu_Aufgabe_C1|Lösung zu Aufgabe C1]] | |
| − | + | [[Einfluss_von_c/Lösung_zu_Aufgabe_C2|Lösung zu Aufgabe C2]] | |
| − | + | ||
| − | + | [[Einfluss_von_c/Lösung_zu_Aufgabe_C3|Lösung zu Aufgabe C3]] | |
| − | + | [[Einfluss_von_c/Lösung_zu_Aufgabe_C4|Lösung zu Aufgabe C4]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
---- | ---- | ||
Aktuelle Version vom 12. Juli 2009, 15:41 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Einfluss von c
|
Wir betrachten nun den Einfluss von
|
|
|
|
Nun betrachten wir den Einfluss von
|
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe C1 ein Hefteintrag "versteckt" ist!
 in
in
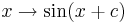 .
.
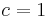 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 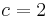 und
und 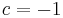 , sowie
, sowie 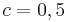 und
und 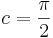 auf den Graphen auswirken und überprüfe deine Vermutung.
auf den Graphen auswirken und überprüfe deine Vermutung. 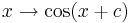 .
.

