Anwendungen in der Physik: Unterschied zwischen den Versionen
K |
K |
||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Trigonometrische Funktionen}} | |
| − | + | ||
| − | + | ||
| Zeile 63: | Zeile 61: | ||
# Übernehme die folgende Zeichnung in dein Heft und vervollständige die Beschriftungen! | # Übernehme die folgende Zeichnung in dein Heft und vervollständige die Beschriftungen! | ||
:[[bild:Sinus.gif|left|400px]] }} | :[[bild:Sinus.gif|left|400px]] }} | ||
| − | ||{{#ev:youtube| | + | ||{{#ev:youtube|JA2FuT_TB7c|150}} |
|} | |} | ||
| Zeile 71: | Zeile 69: | ||
{{Arbeiten|NUMMER=P5 - Zusatzaufgabe|ARBEIT= | {{Arbeiten|NUMMER=P5 - Zusatzaufgabe|ARBEIT= | ||
Bearbeite diesen [http://www.mathe-online.at/lernpfade/harmonischeSchwingung/ Lernpfad] zur harmonischen Schwingung!}} | Bearbeite diesen [http://www.mathe-online.at/lernpfade/harmonischeSchwingung/ Lernpfad] zur harmonischen Schwingung!}} | ||
| − | ||{{#ev:youtube| | + | ||{{#ev:youtube|F-jXwywnBtc|150}} |
|} | |} | ||
---- | ---- | ||
| − | + | <popup name="Lösung zu Aufgabe P1"> | |
| − | + | 1. <math>\ A = 4 cm</math> | |
| + | |||
| + | 2. <math>\ T \approx 0,925 s</math> | ||
| + | |||
| + | 3. <math>f = \frac{1}{T} = \frac{1}{0,925 s} \approx 1,08 Hz </math> | ||
| + | |||
| + | 4. <math>\omega = 2 \pi f = 2 \pi \cdot 1,08 Hz \approx 6,8 \frac{1}{s}</math> oder <math>\omega = \frac{2\pi}{T} = \frac{2\pi}{0,925s} \approx 6,8 \frac {1}{s} </math> | ||
| + | |||
| + | 5. <math>s(t) = 4 \cdot \sin(6,8 t)</math> | ||
| + | </popup> | ||
| + | |||
| + | |||
| + | <popup name="Lösung zu Aufgabe P3"> | ||
| + | |||
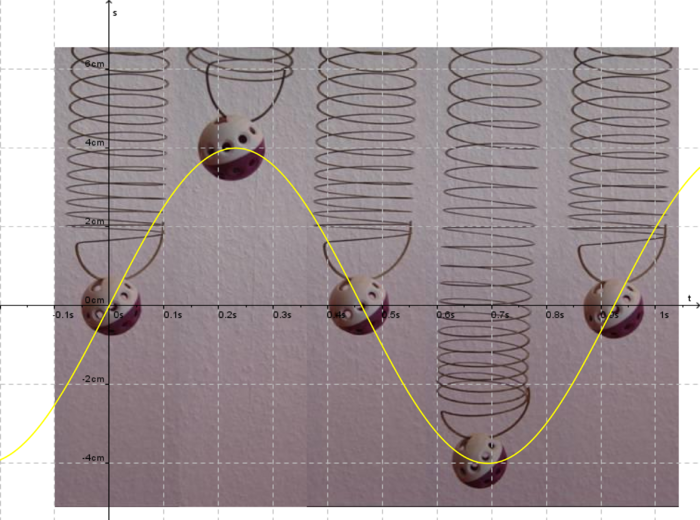
| + | 1. Die Spitzenspannung (Amplitude) beträgt ungefähr 2,3V. | ||
| + | |||
| + | 2. Die Schwinungsdauer beträgt in etwa <math>\ T = 0,4ms</math>. | ||
| + | |||
| + | 3. Es gibt mehrere Möglichkeiten die Frequenz zu bestimmen. So errechnet man z.B. aus der Schwingungsdauer, dass <math> f = \frac{1}{0,4ms}=\frac{1}{\frac{4}{10000}s}=2500Hz=2,5kHz </math> gilt. | ||
| + | </popup> | ||
---- | ---- | ||
Zurück zur [[Trigonometrische Funktionen|Einführung]]! | Zurück zur [[Trigonometrische Funktionen|Einführung]]! | ||
Aktuelle Version vom 3. Juli 2016, 12:34 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Anwendungen in der Physik
|
Hefteintrag: Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben! Es gibt viele periodische Vorgänge, also Vorgänge, die sich nach einer bestimmten Zeit wiederholen. Zeichnet man deren zeitlichen Verlauf auf, so erhält man einen sinusförmigen Graphen. |
| : |
|
| : |
|
|
|
|
Zurück zur Einführung!
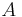 !
!
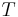 ?
?
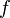 !
!
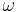 !
!
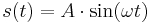 an!
an!
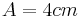
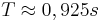
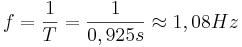
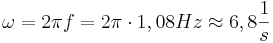 oder
oder 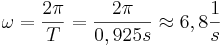
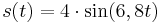
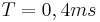 .
.
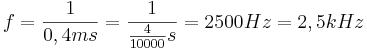 gilt.
gilt.

