Einfluss der Parameter: Unterschied zwischen den Versionen
(→Einfluss der Parameter: Applet verbessert) |
K (Leerzeile eingefügt) |
||
| (7 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Trigonometrische Funktionen}} | |
| − | + | ||
| − | + | ||
| − | + | ||
===FAQ=== | ===FAQ=== | ||
| Zeile 87: | Zeile 84: | ||
{{Arbeiten|NUMMER=1|ARBEIT= | {{Arbeiten|NUMMER=1|ARBEIT= | ||
Welcher Zusammenhang besteht zwischen der Sinus- und der Kosinusfunktion? Zeichne dazu die Graphen der Funktionen <math>\,\!x \rightarrow \sin\left(x+\frac{\pi}{2}\right)</math> und <math>\,\!x \rightarrow \cos(x)</math> in dein Heft oder mit Hilfe von diesem [http://www.gymnasium-walldorf.de/mathematik/trigo_otto/trigo.html Applet] und betrachte sie! Was fällt dir auf? | Welcher Zusammenhang besteht zwischen der Sinus- und der Kosinusfunktion? Zeichne dazu die Graphen der Funktionen <math>\,\!x \rightarrow \sin\left(x+\frac{\pi}{2}\right)</math> und <math>\,\!x \rightarrow \cos(x)</math> in dein Heft oder mit Hilfe von diesem [http://www.gymnasium-walldorf.de/mathematik/trigo_otto/trigo.html Applet] und betrachte sie! Was fällt dir auf? | ||
| − | : | + | :<popup name="Tipp zum Zeichnen ins Heft">Überlege dir zunächst die Lage der Nullstellen und die Größe der Amplitude!</popup> |
}} | }} | ||
||{{#ev:youtube|SQsZVmre3ZI|150}} | ||{{#ev:youtube|SQsZVmre3ZI|150}} | ||
| Zeile 117: | Zeile 114: | ||
|} | |} | ||
| − | <ggb_applet | + | <center> |
| + | <ggb_applet width="690" height="517" version="4.2" ggbBase64="UEsDBBQACAgIADo54kIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIADo54kIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vxbc9u2En5OfwVGT+05EY37pWO346ZNmzS3xunl9KVDkZTEWiIVkrJlTx/OPzx/6SwAUpIlWbFSy3Y5mUkMXgAs8O3ut7uw5MOvZ+MROkuKMs2zow4JcAclWZTHaTY46kyrfld3vv7qs8NBkg+SXhGifl6Mw+qowwPaWYyDu4AwOziNjzox6fdFL+x3VSzCLg9Zr9uL+71uQnHMQkaiqBd2EJqV6ZdZ/iocJ+UkjJKTaJiMwxd5FFZuzmFVTb48ODg/Pw8a6UFeDA4Gg14wK+MOgpVn5VGnvvgSprsy6Jy57hRjcvDbyxd++m6alVWYRUkH2V1N068+e3R4nmZxfo7O07gaHnWk0R00TNLBELYppOqgA9tpAnudJFGVniUlDF26dXuuxpOO6xZm9v0jf4VG8+10UJyepXFSHHVwYAjRRAqluWaUC4AyL9Ikq+q+uJZ50Mx2eJYm535ae+Uk8g6q8nzUC+2MSBj011+IYorRY9sQ31BopPSvsH+GmW+ob7hvhO/D/XDuu3Lfh/s+nIHG0zLtjZKjTj8clQBimvULUOD8vqwuRolbUv1gAQB9DNss00voDPI6yKMOa3+MH3Ps/vttL+2RLEmsiulWgf79krxGmiDyZtLo39ofXshTV+XRa+TpvyWPNPKIWEJT4Mfun/u/jqe8c5FsJ1RXlfgxEiXfItELuF2BHBt1xyIVvguBhwcN7xzWVIPKoe1b+2KVjEtLPsw4/kEECSAZqYAuBCIGGkXhMUVEIC7glmgkbasQU/CCI4Y0sv0IQ45lhIYf3L4jEgmYyz5U2N6DGI4EQ8RxE0fASMjxG3AdZdBDCCRgkJVOrFgmEZdwwzTisEDLbIrY5zAO7kE4RYwgZscShahEkiJl2ZFwS5pS27XDpBRJjKQdCvQI1OhpEUZoxOxuwKkmeZnOaWCYjCZzrTgc02wyrWrs6ufROG5wrPKV7nEenX4zB7t+k4RltdwNosMiBvlocSVEPTochb1kBIH8xFoCQmfhCNyx4yT086xCjRVQ/2xQhJNhGpUnSVXBqBL9GZ6FL8IqmT2F3mUj24l2kfMwmUajNE7D7BcwEzuFnRAtAileBFKujZcS5XkRn1yUYDto9ntS5LAATAJKKGNUEaOwATwv/BsqWCDgsZKMG0m4AMuNQmvzlAeMGq2VVAxjBfEUBl3/zolOzuZbC2dJ2cA/KNJ4+fpZ+U0+iudQT/I0q56Ek2pauKQIomBh93ScDUaJg9ZFDkgvotNePjvxmDI/17uLSWJtwsnvDZ7ko7xAhd0YbGVQtz3fuj52YfNe2PXBrgdulJTG8/fEUNfDtT3ful6gdb+0eqOk2SXBjZi0dERio9aSSzuTOerMOmiapdULf/e//4KNptFpvVnih7yajntgcHMjhg7fpj65somkUFgZyahUBnQv5YpcslHuxRW5HyF1CSXIt8rqt41Lca/+U6e79vrdMKlCm5gJyoTRSgn4aU3IW/uKnR+eJkWWjLw1Z2BQ03xaeveau8ijw2mZvAmr4XEWv00GQA1vQsvOFSzed3Ub8O6eROkYBvrntQpDa14/Axj+aZwMiqTuH45cNuwV7N7iZd9ae+ymelrk42fZ2Tuw3ZWlHh40+zksoyKdWA9BPQgXp8nCCwClEIJNvDwONl/CLiJLfKCJyqqpg8JpNczBOE/S0Vkaoud5GA3TMcwATAK7Q8+noxS4GzzEMsgoGUPeiyrnJ9l0nBRpNDeH2KXUsNpps6FGwdYUUN77E9huxYQWsMLrazwJhaPJ0Omb1P4SXiTFFczcbC/zuBZc9ytHNoNH4xSIvgu+hMbhzDkVCntlPppWUMWAmrJFFePXVjMiwXYDCIZw464u4Eq4uqmfzpI5CwF+6SVY1lUzWTh1BTR9CpVB6ZinqjnGXfyQxnGSzRccZmBZTj9AuBO/YwRBIvEuOB86AQQcuy1ZRa2bD2opaq2WmGKt0VJvVUukLVqiQrdGS2FrtUQ4+SdpaTYpQJqdpka5Dxn4zObpn8++QEcoRP+C9Dn7vAft5zP0bxR98QX8jH1qflXJ/WnmYmRnMdd2jS5lETdRKV5TKdmoUrwFVbEN1evt1yXH83Ufr++rOUO48cZcRrxla5utFf9d5dfJU+lMFSyVaaKlUVJyzLFydksDI5TUBjOuCSSHFBZ6ueShDgub/l+ptPzTlZzspoB+0xJAFRRkhClKNeBqjLkvPJ98CM8Pc+kDgFMERHPMBDPSEK4Ib+DUElOtMDUUqmh2K2hG+XgcZjHK3MnSk7SIoOgF4PKiszjYCLH1fRQSa7EopBZoD+K0at7XFFvPt6YnqCXSaBIWC10lH0eSq5X1gijJBm3RnYnyA+EnSQdJduYAKhGa4brIvMDeWtBl82QGYHV9EUDqR5dkaZFgJ0U6Q8dN/+Om1zHAa0hACMFKC8GENBwI6pjVEo65jdQbKOxYwIsNTufX/T7zWy19uZ2OJ6M0Squ5HkfWIJ9ltn5NXDRbr3hPk2RiDzxeZ++KMCvtr4qulrrXG9Yb56ZXLSpZs6Fvt9vQVV//9iO5k1BvQK59GA7v+ZNywgTmXAvZOLzVH9FUUaIoNntw+Jvp5ftd9PL9J73clV6+20Uv331cbHyIahEBBEXNMGcKa0GpU4sKiGAaG4iMUigm955sPG1FsmHBxJIyopS2v7HGHs0uAdOHHISClWvKDeb63sz8h13M/IfWmLkMOKZg0YoqxgnYemPmRmsNusEECy7p3u38WSvsXAYUyIEzgzFAp7RuzJwqo6gUkEpJrYRF+Z7M/PkuZv68NWZ+l0F2G6I/tsLMCQbghFAcCkUhOVW+eHQncnsqF4+LaMW2f/S14jNfKz5ds/TBrrXi4FOteG2tqE3AhNaCC8mwBldaqxU3mISrFVkz/50Xh9v88EVr/FBwwzXmEpJUQhdnjIYppoSBiK6hw9557WU78BSBlEJiARFaY/vZynn8ZoZASOeSECrx7ZyKbcPzVZvxVAHWBjIiTA0zmu0lG7ouarzwUeOljxqv1qLGcNeoMfwUNa6PGhqYiDAMKTHhkA2zTVFjlcDmJ4wrFPbwgsjrdjjp5mRuTQN757w3rYBzcwkIBTU1BguqMBVQgNzOOcc2NH9qMZprBTW/nQOKm4WQ1z6EvPEh5Ke1EHK6awg5/RRCrv8lFQxkhitONOOMan7jwmOdwB5eBHnbCifVgWCQHWMpiWEcC++kPFBESCIZ4fDK8P0nzSetQFMBbporoSFMEIK5PyoXEECIVlpRKqR23/baE+GtsN1bz3YnazQ3uQHNzZGf3OaHlTbRG/uH0hsPiDZKMmWIMlKZVXrb4FuO3da9ayO72a9ypH1QxA5u9K4VbkRYAFmDYBJzo4WiDScpJqDkxFgYuNz/wcjP7QCTBhysU0CIJRh4SNechAFawygEXQ42SO6Kk955Tvp5jZPe78JJ7z9x0kZOophYUsKaASdpIJe1lGvNtRpKWnGuW6OkX/bvRVuVdWvFjBBESgqlCwbi1k2hDSiDVwlBOcFC7Z+Ufm0FnPZ0URnDORW2GBRU3heev7cGzyuntey+Tr+P/yCtQHT19EKKfSK6+nGA0cUgz1Yi5y8+cv7qzy5+h4Z5uNeyexhOfOcz3/ncd76EBoJA+AfZHmsntfx5BeAmvDby8e2R7xYPR3CgxC451PVGWyYDezdfytkHEorNNrttpTta7cLymi8GmoBTrhSUFlhJA37tLK1LdYClwthgZSDMy+YDvB+jmns+UFlVwvnDUQIPKFGQLwtMGGRLwKze/WFKwhmDWh4ThaGRyn+QsCtlYH8LArkBIcAckrdGLZcPRy2Nb3RNwDSXtogGD8Fa+t9D2o+9S6ohCHLNBCGCq9ZoIdwUWO9LD90t/gEpnVL2iyhUSfttH6cZKgMuBOeMGAHOQZq/B/CPUMzB8hfd3V+/qP8e1Vf/B1BLBwjaLVIxiQsAAD9LAABQSwECFAAUAAgICAA6OeJC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIADo54kLaLVIxiQsAAD9LAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAIAwAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> <br> | ||
| + | </center> | ||
{| | {| | ||
| Zeile 144: | Zeile 143: | ||
---- | ---- | ||
| − | + | <popup name="Lösung zu Aufgabe 1"> | |
| − | + | ||
| − | + | ||
| − | + | Ja genau, die Graphen der beiden angegebenen Funktionen sind identisch. Genauer gesagt: | |
| + | {{Merksatz|MERK= | ||
| + | <span style="background-color:yellow;"> Man erhält den Graphen der Kosinusfunktion, indem man z.B. den Graphen der Sinusfunktion um <math>\frac{\pi}{2}</math> nach links verschiebt. | ||
| + | Deshalb verhält sich die allgemeine Kosinusfunktion bei Variation ihrer Parameter genauso wie die allgemeine Sinusfunktion.}} | ||
| + | </popup> | ||
| − | |||
| + | <popup name="Lösung zu Aufgabe 3"> | ||
| + | |||
| + | Die gesuchten Parameter sind in dieser Reihenfolge <math>\ a, c, d, b</math>. | ||
| + | </popup> | ||
| + | |||
| + | ---- | ||
| + | {| | ||
<span style="background-color:yellow;">Hefteintrag:</span> Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast! Beachte, dass in der Lösung zur Aufgabe 1 auch ein Hefteintrag "versteckt" ist! | <span style="background-color:yellow;">Hefteintrag:</span> Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast! Beachte, dass in der Lösung zur Aufgabe 1 auch ein Hefteintrag "versteckt" ist! | ||
||{{#ev:youtube|vZY8m7O8y1w|150}} | ||{{#ev:youtube|vZY8m7O8y1w|150}} | ||
Aktuelle Version vom 3. Juli 2016, 12:36 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Einfluss der Parameter
|
Hefteintrag: Am besten verwendest du hierfür dein Heft im Querformat, damit du eine Tabelle mit vier Spalten für den Einfluss von |
Einteilung in ABC-Expertenteams
|
Einteilung in 123-Expertenteams
Jetzt noch was zum Knobeln!!!
|
|
Du hast eine Menge über den Einfluss der einzelnen Parameter auf das Aussehen der Graphen herausgefunden. Natürlich können aber die Parameter nicht nur einzeln variiert werden, sondern auch mehrere oder alle gleichzeitig.
|
|
|
|
|
Weiter geht es mit
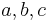 und
und 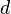 anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
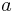
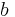

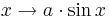
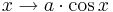 .
.
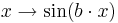
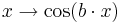 .
.
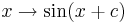
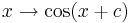 .
.
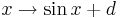
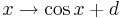 .
.
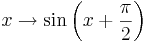 und
und 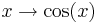 in dein Heft oder mit Hilfe von diesem
in dein Heft oder mit Hilfe von diesem 
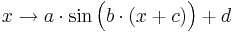
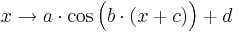
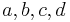 Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt
Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt 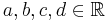
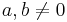
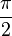 nach links verschiebt.
Deshalb verhält sich die allgemeine Kosinusfunktion bei Variation ihrer Parameter genauso wie die allgemeine Sinusfunktion.
nach links verschiebt.
Deshalb verhält sich die allgemeine Kosinusfunktion bei Variation ihrer Parameter genauso wie die allgemeine Sinusfunktion.
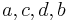 .
.

