|
|
| Zeile 75: |
Zeile 75: |
| | [[Einfluss_von_c/Lösung_zu_Aufgabe_C1|Lösung zu Aufgabe C1]] | | [[Einfluss_von_c/Lösung_zu_Aufgabe_C1|Lösung zu Aufgabe C1]] |
| | | | |
| − | ''Lösung zu Aufgabe C''1: {{versteckt|
| |
| − |
| |
| − | {{Merksatz|MERK=
| |
| − | Man erhält den Graph der Funktion
| |
| − | :<math> x \rightarrow \sin ( x + c ) </math>
| |
| − | aus dem Graph der Sinusfunktion durch Verschiebung in Richtung der <math>\ x</math>-Achse. Genauer:
| |
| − | * <span style="background-color:yellow;"> Ist <math>\ c</math> positiv, so wird der Graph der Sinusfunktion um den Betrag von <math> \ c </math> nach links verschoben.
| |
| − | * Ist <math>\ c</math> negativ, so wird der Graph der Sinusfunktion um den Betrag von <math> \ c </math> nach rechts verschoben.
| |
| − | <math>\ c</math> wird auch als Phasenverschiebung bezeichnet.}}
| |
| − | </span>
| |
| − |
| |
| − | <graphviz>
| |
| − | digraph G {
| |
| − | rankdir=LR;
| |
| − | "Start"-> "c > 0";
| |
| − | "Start"-> "c < 0";
| |
| − | "c > 0"->"Verschiebung nach \n links um |c|";
| |
| − | "Verschiebung nach \n links um |c|" -> "Ziel";
| |
| − | "c < 0"-> "Verschiebung nach \n rechts um |c|";
| |
| − | "Verschiebung nach \n rechts um |c|" -> "Ziel";
| |
| − | }
| |
| − | </graphviz>
| |
| − | [[Bild:N_sin_c.jpg|center]]
| |
| − | }}
| |
| | ||{{#ev:youtube|X-bhGiUinHQ|150}} | | ||{{#ev:youtube|X-bhGiUinHQ|150}} |
| | |} | | |} |
| | | | |
| | [[Einfluss_von_c/Lösung_zu_Aufgabe_C2|Lösung zu Aufgabe C2]] | | [[Einfluss_von_c/Lösung_zu_Aufgabe_C2|Lösung zu Aufgabe C2]] |
| − |
| |
| − | ''Lösung zu Aufgabe C''2: {{versteckt|
| |
| − | Eine mögliche Begründung:
| |
| − |
| |
| − | <math>\ \sin( x + c )=0 </math>
| |
| − |
| |
| − | <math> \Leftrightarrow x + c = k \cdot \pi; k \in \Z </math>
| |
| − |
| |
| − | <math> \Leftrightarrow x = k \cdot \pi - c </math>
| |
| − |
| |
| − | Die Bestimmung der Nullstellen von <math> x \rightarrow \sin ( x + c ) </math> und Vergleich mit den Nullstellen der Sinuskurve zeigt, dass jeder Funktionswert für <math>\ c > 0 </math> bereits ein Stück weiter links angenommen wird. Genauer, der Graph wird also für <math>\ c > 0</math> um <math>\ c </math> nach links verschoben und für <math>\ c < 0 </math> entsprechend nach rechts.
| |
| − | }}
| |
| | | | |
| | [[Einfluss_von_c/Lösung_zu_Aufgabe_C3|Lösung zu Aufgabe C3]] | | [[Einfluss_von_c/Lösung_zu_Aufgabe_C3|Lösung zu Aufgabe C3]] |
| − |
| |
| − | ''Lösung zu Aufgabe C''3: {{versteckt|
| |
| − | Die allgemeine Kosinusfunktion verhält sich bei Variation von <math> \ c </math> genauso wie die allgemeine Sinusfunktion.
| |
| − |
| |
| − | [[Bild:N_cos_c.jpg|center]]
| |
| − | }}
| |
| | | | |
| | ---- | | ---- |
Version vom 28. Februar 2009, 00:01 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Einfluss von c
|
Wir betrachten nun den Einfluss von  in
 .
|
|
Aufgabe C2 
Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen!
|
|
|
|
Nun betrachten wir den Einfluss von in
 .
Aufgabe C3
Öffne dieses GeoGebra-Applet und bearbeite damit die Aufgaben C1/ 2-4 noch einmal.
|
|
|
Lösung zu Aufgabe C2
Lösung zu Aufgabe C3
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe C1 ein Hefteintrag "versteckt" ist!
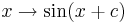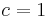ein. Wie ändert sich der Graph? 
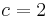und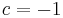 
, sowie 
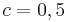und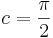 
auf den Graphen auswirken und überprüfe deine Vermutung. 
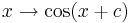