Diskret - kontinuierlich: Unterschied zwischen den Versionen
(→Logistisches Wachstum - beschränktes Wachstum) |
(→Logistisches Wachstum - beschränktes Wachstum) |
||
| Zeile 166: | Zeile 166: | ||
<math> | <math> | ||
| − | f=\frac{1}{1+e^{-r\cdot t +C}} | + | f(t)=\frac{1}{1+e^{-r\cdot t +C}} |
</math> | </math> | ||
Version vom 29. März 2009, 09:47 Uhr
Matthias Kittel und Walter Wegscheider
|
Über diesen Lernpfad
Schüler/innen sollen sich mit der Beschreibung von dynamischen Vorgängen beschäftigen und den Unterschied zwischen diskreten Vorgängen (Beschreibung über Differenzengleichungen) und kontinuierlichen Vorgängen (Beschreibung über Differentialgleichungen) kennen lernen. Kompetenzen
|
Inhaltsverzeichnis |
Rekursive Beschreibung von Veränderungen
Numerische Näherung - Heronverfahren
Radioaktiver Zerfall
Für Beispiele zum radioaktiven Zerfall siehe hier
Räuber-Beute-Modell
Zum Thema Räuber-Beute-Modell geht es hier.
Differenzengleichung
Begriffsbildung
Eine Differenzengleichung ist eine Möglichkeit, dynamische Systeme abzubilden. Dabei wird eine Folge von diskreten (einzeln betrachtbaren, "abzählbaren") Ereignissen rekursiv definiert. Jedes Folgenglied ist daher eine Funktion der vorhergehenden Folgenglieder.
Form: 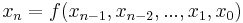
für natürliche Zahlen n.
Die Veränderung wird durch den Differenzenquotienten angegeben:
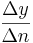
mit 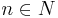
Dabei entspricht:
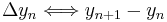 und damit beispielsweise
und damit beispielsweise 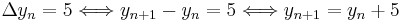
Links:
- http://statmath.wu-wien.ac.at/~leydold/MOK/HTML/node187.html, Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997
Marktgleichgewicht - Cobweb-DIagramm
Cobweb / Spinnwebdiagramme stellen eine gute Möglichkeit dar, Rekursionen darzustellen.
Links:
- Spinnwebdiagramme - Lineare Differenzengleichungen 1. Ordnung mit GeoGebra: http://www.geogebra.org/de/wiki/index.php/Lineare_Differenzengleichung_1._Ordnung
Von der diskreten zur kontinuierlichen Veränderung
Exponentielles Wachstum - Lebensmittelkontrolle
In Österreich ist es üblich, dass Lebensmittel verarbeitende und verkaufende Betriebe der Lebensmittelkontrolle obliegen (sie Bundesministerium für Gesundeheit. Lebensmittel dürfen nämlich einen bestimmten Grenzwert an Bakterien nicht überschreiten, wenn sie verkauft werden sollen. Lebensmittelkontrollore überwachen die korrekt Verwahrung der Speisen und Getränke.
Egal um welche Art von Keimen es sich handelt, die Vermehrungsrate ist gigantisch. Aus diesem Grund verwendet man häufig eine Exponenzialfunktion, um das Wachstum zu beschreiben. Mit Hilfe des Zusammenhangs 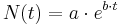 lässt sich diese Wachstum beschreiben.
lässt sich diese Wachstum beschreiben.
Diese Problem lässt sich mittel Differenzengleichung 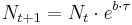 modellieren, wobei
modellieren, wobei 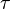 der Zeitschritt ist. Dies ist in der Tabellekalkulationsmappe Lebensmittel.xls realisiert. In der Arbeitsmappe befindet sich ein Arbeitsblatt, das zur Rückrechnung einer Keimanzahl verwendet werden kann. So kann überprüft werden, ob eine Lebensmittelprobe zum Zeitpunkt des Verkaufs noch genießbar war.
Es lassen sich die Anfangsanzahl der Keime sowie die Vermehrungskonstante variieren. Die Ergebnisse sing graphisch und in einer Tabelle dargestellt.
der Zeitschritt ist. Dies ist in der Tabellekalkulationsmappe Lebensmittel.xls realisiert. In der Arbeitsmappe befindet sich ein Arbeitsblatt, das zur Rückrechnung einer Keimanzahl verwendet werden kann. So kann überprüft werden, ob eine Lebensmittelprobe zum Zeitpunkt des Verkaufs noch genießbar war.
Es lassen sich die Anfangsanzahl der Keime sowie die Vermehrungskonstante variieren. Die Ergebnisse sing graphisch und in einer Tabelle dargestellt.
|
Merke:
Antibakterienvermehrungstheorem: |
Radioaktiver Zerfall - analytische Herleitung
Die Gleichung 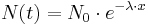 ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften Schulstufe ist es nun mit Hilfe der Integralrechung möglich, ausgehend vom Ansatz
ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften Schulstufe ist es nun mit Hilfe der Integralrechung möglich, ausgehend vom Ansatz 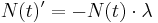 obige Relationen per Differentialgleichung analytisch herzuleiten.
Unter Rad_zerfall_analytisch.pdf ist diese Herleitung Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und dann der Bezug auf die Anwendung beim radioaktiven Zerfall hergestellt.
obige Relationen per Differentialgleichung analytisch herzuleiten.
Unter Rad_zerfall_analytisch.pdf ist diese Herleitung Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und dann der Bezug auf die Anwendung beim radioaktiven Zerfall hergestellt.
Zusätzlich sind drei Standardaufgaben angegeben, um die Verwendung der Gleichung zu wiederholen.
Beispiele zum radioaktiven Zerfall
|
Merke:
Halbwertszeit: Der Zeitraum, in dem eine (meist exponentiell) abfallende Größe auf die Hälfte ihres Anfangswertes abgesunken ist. Die physikalische Halbwertszeit ist die für jedes Isotop eines radioaktiven Elementes charakteristische Zeitdauer, in der von einer ursprünglichen vorhandenen Anzahl radioaktiver Kerne bzw. instabilen Elementarteilchen die Hälfte zerfallen ist (entnommen aus Brockhaus in 5 Bänden, zweiter Band). |
|
Jod-131 hat eine Halbwertszeit von 8 Tagen. Berechne den Parameter λ (Basiszeiteinheit 1 Tag und 1 Jahr) in der Zerfallsgleichung auf 6 gültige Nachkommastellen! |
|
Von Kobalt-60 ist nach 3,88 Jahren 40% des Ausgangsmaterials zerfallen. Wie groß ist die Halbwertszeit dieses Isotops? |
|
Von 24000 Cäsium-137-Kernen sind nach einer bestimmten Zeit |
Aufgaben im pdf-Format
Die Angaben zu den Aufgaben findet man unter Bsp_rad_zerfall.pdf (43 kb).
Lösungen im pdf-Format
Die Lösungen zu diesen Aufgaben findet man unter Lösungen zu Bsp_rad_zerfall.pdf (59 kb).
Abbau von Giftstoffen
Zusammenfassung des Giftstoffproblems
analytische Lösung der Differenzialgleichungen für den Abbau von Giftstoffen
Derive-Datei zum Abbau von Giftstoffen
Logistisches Wachstum - beschränktes Wachstum
Als logistische Gleichung wird eine Differenzengleichung der Form 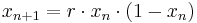 . Die zugehörige Differenzialgleichung (DGLG) sieht folgendermaßen aus:
. Die zugehörige Differenzialgleichung (DGLG) sieht folgendermaßen aus: 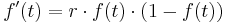 Diese DGLG kann analytisch gelöst werden, zur Vereinfachung wird statt
Diese DGLG kann analytisch gelöst werden, zur Vereinfachung wird statt 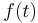
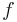 geschrieben:
geschrieben:
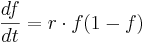
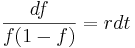
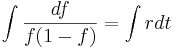
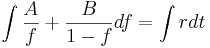
Mittels Partialbruchzerlegung ermittelt man für 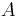 und
und 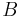 jeweils der Wert
jeweils der Wert 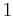 .
.
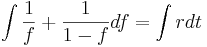
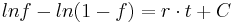
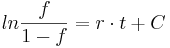
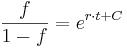
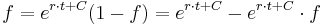
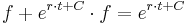
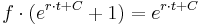
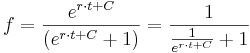
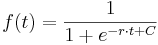
Ein-Lebewesen-Modell nach Verhulst
Erläuterungen, Informationen und Aufgaben zum Ein-Lebewesen-Modell findet man hier.
Weitere Beispiele
- Bernd Huhn, Sonja Woltzen, Lehrer-Online, Fall mit Reibung - Ein Sprung aus 40.000m Höhe, 2005
- Josef Lechner, Freier Fall mit Luftwiderstand, ACDCA 1998
Differentialgleichungen
Begriffsbildung
Als (gewöhnliche) Differenzialgleichung (DGLG) wird eine Gleichung bezeichnet, die neben einer Unbekannten 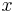 auch deren Ableitung(en)
auch deren Ableitung(en) 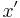 (
(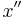 , ...) enthält. Gelöst wird eine DGLG mittels Integralrechnung.
, ...) enthält. Gelöst wird eine DGLG mittels Integralrechnung.
Die Lösung einer DGLG ist nicht wie bei einer herkömmlichen Gleichung eine Zahl, sondern eine Funktion, genauer eine Funktionenschar, die aus unendlich vielen Funktionen besteht. Da beim unbestimmten Integrieren immer eine Integrationskonstante auftritt, muss eine Zusatzinformation (Anfangsbedingung) gegeben sein, um die Konstante zu bestimmen.
Erst durch die Anfangsbedingung, die einem Punkt auf dem Graphen der Lösungsfunktion entspricht, kann die Lösungsfunktion exakt bestimmt werden. Die Lösung ist nun eine spezielle Funktion!
DGLG können in allen Bereichen des Lebens angetroffen werden, besonders in den Naturwissenschaften oder der Wirtschaft und dem Sport. In allen Zusammenhängen, bei denenen es um Veränderungen geht, kommen DGLG zur Anwendung.
Eine Übersicht über die Klassifikation von DGLG findet man unter http://www.math.tu-berlin.de/geometrie/Lehre/SS05/GDglmA/skriptKlassif.pdf
Links:
- http://statmath.wu-wien.ac.at/~leydold/MOK/HTML/node175.html, Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997
Lösung einfacher Differentialgleichungen
Ausblick
Näherungsverfahren
Bisher wurde die Lösung der betrachteten Differentialgleichungen über Integration vorgestellt. Man versucht dabei, eine mathematisch exakte (und bis auf die Integrationskonstante eindeutige) Lösung formal zu bestimmen. Die gefundene Lösungsfunktion liefert eine vollständige Beschreibung des betrachteten Problems über den gesamten definierten Verlauf. In den meisten Fällen sind diese gefundenen Lösungsfunktionen auch stetig und bieten daher eine kontinuierliche Problemlösung.
Es gibt aber viele Integrale und damit Differentialgleichungen, die man nur äußerst mühselig oder in vielen Fällen überhaupt nicht exakt lösen kann!
Man geht daher oft den - nebenbei auch bei der Automatisation der Lösungsalgorithmen mit dem Computer meist schnelleren - Weg, die Probleme näherungsweise zu lösen. Man setzt also auf Näherungsverfahren, die das vorliegende Problem für eine diskrete (endliche) Zahl von Punkten möglichst genau lösen. Man ersetzt also die vollständige Integration einer Funktion durch die näherungsweise Berechnung (des bestimmten Integrals) in einem bestimmten Bereich, für den man sich interessiert. Für diese Näherung / Diskretisierung gibt es verschiedene, unterschiedlich genaue - unterschiedlich komplexe Verfahren.
Grundsatz: Der Differentialquotient wird näherungsweise durch den dazugehörigen Differentenquotienten beschrieben.
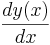 beschrieben durch
beschrieben durch
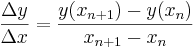
Die bekanntesten Näherungsverfahren
- Euler-Cauchy-Verfahren
- Runge-Kutta-Verfahren
Eine Beschreibung der Verfahren finden Sie bei Ulrich Streit, Skript zur Übung "Werkzeuge zur numerischen Modellierung", 1999
Links:
- Josef Lechner, Von Euler-Cauchy zu Runge-Kutta, ACDCA 1998
- Urs Oswald, H.R. Schneebeli, Kugelstoßen mit Luftwiderstand, TI-Nachrichten 2/04
- H. Kohorst, Ph. Portscheller, P. Goldkuhle, Modellbildung und Simulation - NRW-Bildungsserver learn:line
Visualisierung über Richtungsfelder
© 2009, Projekt "Medienvielfalt im Mathematikunterricht"

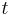 21771 Kerne zerfallen. Die Halbwertszeit des Isotops beträgt 2,1 Jahre. Berechne
21771 Kerne zerfallen. Die Halbwertszeit des Isotops beträgt 2,1 Jahre. Berechne 
