Wurzelfunktionen Eigenschaften: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 4: | Zeile 4: | ||
Der Differenzenquotient <math>k = \frac{\bigtriangleup y}{\bigtriangleup x}</math> = <math>\frac{f(x_2)-f(x_1)}{x_2-x_1}</math> ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x. | Der Differenzenquotient <math>k = \frac{\bigtriangleup y}{\bigtriangleup x}</math> = <math>\frac{f(x_2)-f(x_1)}{x_2-x_1}</math> ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x. | ||
<br> | <br> | ||
| − | * Er gibt die '''Steigung einer Sekante''' durch die Punkte <math>\left( x_1 | + | * Er gibt die '''Steigung einer Sekante''' durch die Punkte <math>\left( x_1 \mid f(x_1)\right)</math> und <math>\left( x_2/f(x_2)\right)</math> |
* Er ermöglicht die Berechnung des Steigungswinkels. | * Er ermöglicht die Berechnung des Steigungswinkels. | ||
* Er gibt die '''mittlere Änderungsrate''' an. | * Er gibt die '''mittlere Änderungsrate''' an. | ||
Version vom 11. Mai 2012, 08:44 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Der Differenzenquotient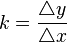 
= 
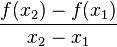ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x.
- Er gibt die Steigung einer Sekante durch die Punkte
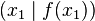und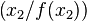 
- Er ermöglicht die Berechnung des Steigungswinkels.
- Er gibt die mittlere Änderungsrate an.
