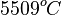Wurzelfunktion Übungen 2
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Bei den Übungen zur Wurzelfunktion lernst du weitere sich aus ihr ergebene Funktionen kennen.
|
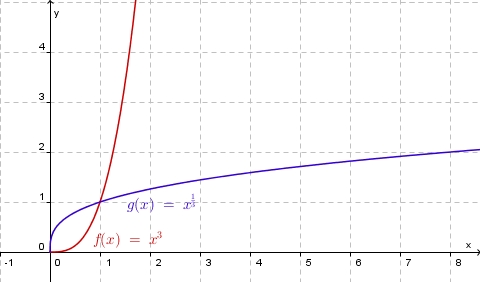
Zeichne den Graphen der Funktionen |
|
Bestimme die natürliche Zahl n so, dass der Graph der Funktion der Funktion Bearbeite von dieser Webseite die ersten 3 Aufgaben. |
|
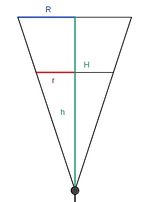
Ein Sektglas ist kegelförmig. Der Radius R der Deckfläche ist 5 cm, die Höhe H des Kegels 8 cm. Bei der Füllhöhe h = 7,88 cm ist das Glas genau mit 0,2 l gefüllt. (1 l = 1 dm³) 1. Nun interessiert die Frage, bei welcher Höhe ist das Glas halb voll? Mit h bezeichnen wir die Füllhöhe. a) Gib eine Formel für das Volumen V mit Füllhöhe h an. b) Bestimme mit Hilfe des Strahlensatzes einen Zusammenhang zwischen h, H , R und r. c) Gib nun eine Abhängigkeit des Volumens von h an. d) Löse dein Ergebnis aus 3. nach h auf. e) Bestimme zu 2. Die Abhängigkeit der Füllhöhe vom Volumen kann man auch schreiben als a) Leite aus b) Gib für die Funktion Im folgenden Applet ist die Füllhöhe h als Funktion des Quotienten
c) Bestimme graphisch und rechnerisch bei welcher Höhe h das eingefüllte Volumen 25%, 40%, 75% des Glasvolumens ist. |
|
Franziska und Max studieren Medizin im 1. Semester. In der Anfangsvorlesung lernen sie, dass das Flüssigkeitsvolumen 1. Stelle diesen Sachverhalt als Formel dar! 2. Löse diese Gleichung nach r auf und gib jene Funktionsgleichung an, die dem Volumen 3. Wie ändert sich das Blutvolumen, das durch eine Ader fließt, wenn sich der Gefäßradius um 4. Um wieviel darf der Radius 5. Um wieviel darf der Radius |
|
Die zwei österreichischen Physiker Josef Stefan und Ludwig Boltzmann fanden das nach ihnen benannte Strahlungsgesetz. Es besagt, dass die Strahlungsleistung P einer Lichtquelle proportional zur 4. Potenz der Temperatur T dieser Lichtquelle (T gemessen in der absoluten Kelvin-Temperatur) ist. Dieser Sachverhalt wird durch die Formel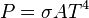 In dieser Formel ist a) Löse die Gleichung nach T auf und gib jene Funktionsgleichung an, die der Strahlenleistung b) Die Strahlungsleistung der Sonne beträgt Wie groß ist die Oberflächentemperatur in K (und in °C) auf der Sonne? |
Aufgabe 22
Aufgabe 23
a) n = 4 und ![f(x) = \sqrt[4]{x}](/images/math/2/6/d/26ddeb554beea308d2b59b993c025967.png)
b) n = 5 und ![f(x) = \sqrt[5]{x}](/images/math/2/d/5/2d56125dbac62dc1e12dfab7d98d7228.png)
![f(x) = \sqrt[3]{x}](/images/math/b/5/9/b592d4981e272d6edd9ec4263a0a874b.png)
Aufgabe 24
1a) 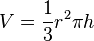
1b) 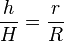
1c) Mit 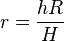 ergibt sich
ergibt sich 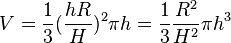
1d) ![h = \sqrt[3]{\frac{3VH^2}{R^2 \pi}}](/images/math/1/c/7/1c76d5cd8d856278b0a7cdd09c3feb14.png)
1e) 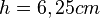
Ein kegelförmiges Sektglas ist also bei rund 80% der Füllhöhe halb voll.
2a) 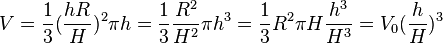 , wobei
, wobei 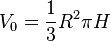 das Glasvolumen ist.
das Glasvolumen ist.
Nach h auflösen: ![h =H \sqrt[3]{\frac{V}{V_0}}](/images/math/c/3/f/c3f29c39c02cdb4f7adf1a39d6129e38.png)
2b) ![h(q) = 8 \sqrt[3]{q}](/images/math/6/e/d/6edfdc93fbe23ecab531ddcecb5ab58d.png) ;
; ![D=[0;1]](/images/math/0/f/3/0f31bf13768b8c843ad5d580e6c74910.png) und
und ![W = [0;8]](/images/math/a/6/5/a650ce449df642c610cb59a25e3ed81d.png)
Aufgabe 25
1. 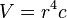 wobei
wobei  eine Konstante ist.
eine Konstante ist.
2. ![r = \sqrt[4]{\frac{V}{c}}](/images/math/a/5/1/a51b89e5f7a48f63d2efb0df2e2b62bd.png)
3. a) Vermehrung um 46%; 506%, 1600%
b) Verminderung um 35%, 93,75%, 100%
4. a) 2,4%
b) 11%
5. a) 2,6%
b) 16%
Aufgabe 26
Zurück zu allgemeinen Wurzelfunktion
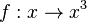 im Intervall
im Intervall ![\left[ 0, 2 \right]](/images/math/2/f/e/2fea535667cede03eab04adf79d41e63.png) und
und ![g:x \rightarrow \sqrt[3]{x}](/images/math/8/3/3/8330b0e6165fadd7edff5e254cd144d3.png) im Intervall
im Intervall ![\left[ 0, 8\right]](/images/math/8/6/c/86c95bc7840195337110a50bd70dd299.png)
![f: x \rightarrow \sqrt[n]{x}](/images/math/1/4/c/14cf23945ed845ea63890d36ad846bcf.png) durch den Punkt
durch den Punkt 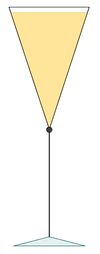
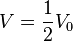 die passende Höhe h.
die passende Höhe h.
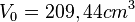 . Es kommt im wesentlichen auf den Quotienten
. Es kommt im wesentlichen auf den Quotienten 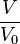 an, den wir mit
an, den wir mit 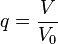 bezeichnen.
bezeichnen.
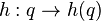 die Funktionsgleichung, die Definitions- und die Wertemenge an.
die Funktionsgleichung, die Definitions- und die Wertemenge an.
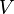 , das bei konstantem Druck pro Zeiteinheit durch eine Röhre mit Radius
, das bei konstantem Druck pro Zeiteinheit durch eine Röhre mit Radius  fließt, proportional zur 4. Potenz des Radius ist. (
fließt, proportional zur 4. Potenz des Radius ist. (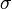 die Stefan-Boltzmann-Konstante
die Stefan-Boltzmann-Konstante 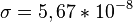 mit der Einheit
mit der Einheit 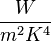 .
.
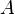 ist die Oberfläche der Lichtquelle.
ist die Oberfläche der Lichtquelle.
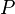 die Temperatur
die Temperatur 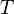 der Lichtquelle zuordnet!
der Lichtquelle zuordnet! 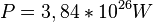 .
.
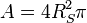 modelliert werden.
modelliert werden.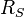 ist circa das 109-fache des Erdradius (6370km).
ist circa das 109-fache des Erdradius (6370km).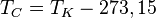 verwenden.
verwenden.
![T = \sqrt[4]{\frac{P}{A\sigma}}](/images/math/a/6/1/a61d079fa2ed36452b2030f1dfbc9bfe.png)
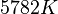 bzw.
bzw.