Wurzelfunktionen Eigenschaften: Unterschied zwischen den Versionen
| Zeile 15: | Zeile 15: | ||
Gib den Steigungswinkel der Sekante an! | Gib den Steigungswinkel der Sekante an! | ||
| − | <br>Löse die | + | <br>Löse die Aufgabe mithilfe von GeoGebra oder einer Tabellenkalkulation!<br> |
}} | }} | ||
| Zeile 28: | Zeile 28: | ||
a) Dem Oberflächeninhalt <math>A</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | a) Dem Oberflächeninhalt <math>A</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
b) Dem Volumen <math>V</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | b) Dem Volumen <math>V</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=16| ARBEIT= | ||
| + | Gib für die folgenden zwei funktionalen Abhängigkeiten | ||
| + | |||
| + | # die Funktionsgleichung an und | ||
| + | # skizziere den charakteristischen Verlauf der beiden Funktionsgraphen! | ||
| + | <br> | ||
| + | a) Dem Oberflächeninhalt <math>A = 36</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
| + | b) Dem Volumen <math>V = 16</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
}} | }} | ||
Version vom 11. Mai 2012, 08:12 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Der Differenzenquotient 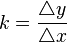 =
= 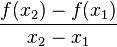 ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x.
ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x.
- Er gibt die Steigung einer Sekante durch die Punkte
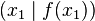 und
und 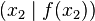
- Er ermöglicht die Berechnung des Steigungswinkels.
- Er gibt die mittlere Änderungsrate an.
|
Zeichne den Graphen der Funktionen Gib den Steigungswinkel der Sekante an!
|
|
Gib für die folgenden zwei funktionalen Abhängigkeiten
|
|
Gib für die folgenden zwei funktionalen Abhängigkeiten
|
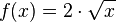 und ermittle die Steigung der Sekante durch die Punkte
und ermittle die Steigung der Sekante durch die Punkte 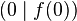 und
und 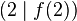 !
!
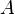 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius  zugeordnet.
zugeordnet.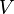 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius 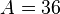 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius 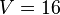 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius 
