Pool 1: Unterschied zwischen den Versionen
(→Logistische Abbildung) |
(→Logistische Abbildung) |
||
| Zeile 24: | Zeile 24: | ||
<font color="#004400">[Aufgabe für xxxer-Gruppe]</font> [Matthias] | <font color="#004400">[Aufgabe für xxxer-Gruppe]</font> [Matthias] | ||
| − | [[images/c/cb/Ein_lebewesen_verhulst_analyt.xls]] | + | [[medienvielfalt/images/c/cb/Ein_lebewesen_verhulst_analyt.xls]] |
Stichworte: Verschiedene Aufgaben für verschiedene Parameter- und Anfangswerte (manche oszillierend, manche chaotisch), visualisieren! Dann die Ergebnisse zusammenführen und beschreiben, dass/wie das Verhalten vom Parameter abhängt. | Stichworte: Verschiedene Aufgaben für verschiedene Parameter- und Anfangswerte (manche oszillierend, manche chaotisch), visualisieren! Dann die Ergebnisse zusammenführen und beschreiben, dass/wie das Verhalten vom Parameter abhängt. | ||
Version vom 26. November 2008, 19:24 Uhr
Lernpfad zur Schnittstelle Sekundarstufe 2 - Universität
Aufgabenpool 1
Startseite des Lernpfads | Aufgabenpool 2 | Didaktischer Kommentar
Inhaltsverzeichnis |
Differentialgleichung versus Differenzengleichung
[Aufgabe für 2er-Gruppe] [Walter]
Stichworte: Ein Problem, das sowohl mit DGL als auch mit Differenzengleichung gelöst werden kann. Beide Partner arbeiten zuerst selbständig, führen dann ihre Ergebnisse zusammen und diskutieren sie.
Integrationsverfahren vergleichen
[Aufgabe für xxxer-Gruppe] [Matthias]
Stichworte: analytische / näherungsweise mit Taylorpolynomen / näherungsweise numerisch. Mögliche Tools: CAS, Tabellenkalkulation.
Logistische Abbildung
[Aufgabe für xxxer-Gruppe] [Matthias]
medienvielfalt/images/c/cb/Ein_lebewesen_verhulst_analyt.xls
Stichworte: Verschiedene Aufgaben für verschiedene Parameter- und Anfangswerte (manche oszillierend, manche chaotisch), visualisieren! Dann die Ergebnisse zusammenführen und beschreiben, dass/wie das Verhalten vom Parameter abhängt. Mögliche Tools: CAS, Tabellenkalkulation.
Ein bisschen Relativitätstheorie
[Aufgabe für 2er-Gruppe] [Franz]
Die Funktion
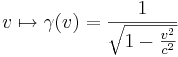
spielt in der Speziellen Relativitätstheorie eine wichtige Rolle. Die Variable 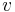 steht für die Geschwindigkeit, mit der sich ein Körper (relativ zu einem Bezugssystem) bewegt, die Konstante
steht für die Geschwindigkeit, mit der sich ein Körper (relativ zu einem Bezugssystem) bewegt, die Konstante 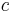 bezeichnet die Lichtgeschwindigkeit.
Bearbeitet zunächst getrennt folgende Fragestellungen:
bezeichnet die Lichtgeschwindigkeit.
Bearbeitet zunächst getrennt folgende Fragestellungen:
- a.) Wie verhält sich die gegebene Funktion für Geschwindigkeiten
 , deren Betrag sehr viel kleiner als die Lichtgeschwindigkeit sind (
, deren Betrag sehr viel kleiner als die Lichtgeschwindigkeit sind ( )? Erstelle eine Näherungsformel
)? Erstelle eine Näherungsformel 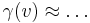 (Reihenentwicklung bis zur Ordnung
(Reihenentwicklung bis zur Ordnung 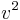 )! Wie sieht der Graph der Funktion in diesem Bereich aus?
)! Wie sieht der Graph der Funktion in diesem Bereich aus?
- b.) Wie verhält sich die gegebene Funktion für Geschwindigkeiten
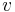 , die in der Nähe der Lichtgeschwindigkeit liegen (
, die in der Nähe der Lichtgeschwindigkeit liegen (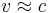 , wobei aber
, wobei aber 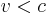 sein soll)? Erstelle eine Näherungsformel
sein soll)? Erstelle eine Näherungsformel 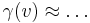 ! Hier ein Tipp:
! Hier ein Tipp: 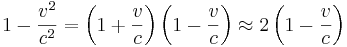 .
.
Setzt euch danach wieder zusammen, diskutiert eure Ergebnisse und führt sie zusammen:
- Wie sieht der Graph der gesamten Funktion aus? (Welche Definitionsmenge wird man sinnvollerweise für sie wählen?)
- Wie passt dieser Graph mit den Graphen der (von euren getrennt erhaltenen) Näherungsfunktionen zusammen? Stellt alle drei Graphen in einem Diagramm dar! Verwendet als Tool einen Punktionsplotter oder ein Programm, das einen solchen enthält! Überlegt euch, wie ihr die Einheiten auf den Achsen wählt, damit das Diagramm möglichst aussagekräftig wird!
- Illustriert anhand einiger Werte von
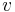 (z.B. die Geschwindigkeit eines Fußgängers, eines Flugzeugs, 90% der Lichtgeschwindigkeit, 99% der Lichtgeschwindigkeit...) wie gut eure Näherungsformeln sind!
(z.B. die Geschwindigkeit eines Fußgängers, eines Flugzeugs, 90% der Lichtgeschwindigkeit, 99% der Lichtgeschwindigkeit...) wie gut eure Näherungsformeln sind!
Wenn das alles geklärt ist, könnt ihr ein bisschen Relativitätstheorie betreiben:
- Die (relativistische) Gesamtenergie eines Körpers der Masse
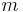 , der sich mit der Geschwindigkeit
, der sich mit der Geschwindigkeit 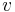 bewegt, ist durch
bewegt, ist durch 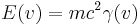 gegeben. Wie verhält sich
gegeben. Wie verhält sich 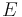 für kleine Geschwindigkeiten? Erinnert euch das Ergebnis an etwas, das ihr in eurem Physikunterricht gelernt habt? Wie verhält sich
für kleine Geschwindigkeiten? Erinnert euch das Ergebnis an etwas, das ihr in eurem Physikunterricht gelernt habt? Wie verhält sich 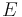 für große Geschwindigkeiten? (Damit könnt ihr argumentieren, dass kein Körper auf Lichtgeschwindigkeit beschleunigt werden kann!)
für große Geschwindigkeiten? (Damit könnt ihr argumentieren, dass kein Körper auf Lichtgeschwindigkeit beschleunigt werden kann!)
- Zwillingsparadoxon: Alice und Bob sich gleich alt. Alice unternimmt eine Reise durchs All mit Geschwindigkeit
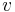 , während Bob auf der Erde zurückbleibt. Als Alice zurückkehrt, stellen die beiden fest, dass Alice jünger geblieben ist. Ist für Bob die Zeit
, während Bob auf der Erde zurückbleibt. Als Alice zurückkehrt, stellen die beiden fest, dass Alice jünger geblieben ist. Ist für Bob die Zeit 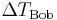 vergangen und für Alice die Zeit
vergangen und für Alice die Zeit 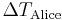 , so ist sagt die Relativitätstheorie die Beziehung
, so ist sagt die Relativitätstheorie die Beziehung 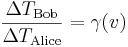
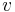 abgeschätzt werden kann!
abgeschätzt werden kann!
Epidemie
[Aufgabe für xxxer-Gruppe] [Peter]
xxx
Elastizität
[Aufgabe für xxxer-Gruppe] [Peter]
xxx
Zentralmaße vergleichen
[Aufgabe für xxxer-Gruppe] [Walter, mgl.weise Josef]
xxx
Streuungsmaße vergleichen
[Aufgabe für xxxer-Gruppe] [Walter, mgl.weise Josef]
xxx
Rekursionsverfahren vergleichen
[Aufgabe für xxxer-Gruppe] [Walter, mgl.weise Josef]
xxx

