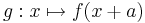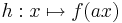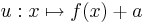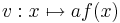Pool 2: Unterschied zwischen den Versionen
(→Das Integral) |
(→Funktionstypen) |
||
| Zeile 135: | Zeile 135: | ||
<font color="#004400">[Aufgabe für 2er- oder 3er-Gruppe]</font> [Matthias] | <font color="#004400">[Aufgabe für 2er- oder 3er-Gruppe]</font> [Matthias] | ||
| + | Eine klassische Aufgabe in der Schule ist in Österreich eine '''Kurvendiskussion'''. Dabei werden die Eigenschaften von Funktionen untersucht. Die zu untersuchenden Funktionen kommen aus den unterschiedlichen Bereichen der Wissenschaft, sehen verschieden aus und besitzen daher auch klassizifierbare Eigenschaften. | ||
| + | |||
| + | Eine Kurvendiskussion besteht aus Punkten, die oft unterschiedlich gruppiert werden, aber im Prinzip dasselbe darstellen. | ||
| + | |||
| + | [http://wikis.zum.de/medienvielfalt/images/a/a8/Kurvendiskussion_fkt_uebersicht_mv.pdf Übersicht über Funktioneneigenschaften] | ||
Stichworte: Welche Typen von Funktionen gibt es, was sind ihre charakteristischen Eigenschaften? | Stichworte: Welche Typen von Funktionen gibt es, was sind ihre charakteristischen Eigenschaften? | ||
Version vom 27. November 2008, 22:21 Uhr
Lernpfad zur Schnittstelle Sekundarstufe 2 - Universität
Aufgabenpool 2
Startseite des Lernpfads | Aufgabenpool 1 | Didaktischer Kommentar
Inhaltsverzeichnis |
Text korrigieren: Radioaktiver Zerfall
[Aufgabe für 2er- oder 3er-Gruppe] [Franz]
Stellt euch vor, ihr findet bei einer Internetrecherche zum Thema "mathematische Beschreibung des radioaktiven Zerfalls" den folgenden Text:
- Die Funktion
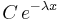 nähert sich für große
nähert sich für große 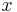 der
der 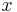 -Achse an. Auf der anderen Seite kommt sie von unendlich großen Werten herunter, bis sie bei
-Achse an. Auf der anderen Seite kommt sie von unendlich großen Werten herunter, bis sie bei 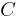 die
die 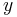 -Achse schneidet. Daher beschreibt sie eine exponentielle Abnahme, in welchem Fall man
-Achse schneidet. Daher beschreibt sie eine exponentielle Abnahme, in welchem Fall man 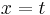 setzen muss. Beim radioaktiven Zerfall ist
setzen muss. Beim radioaktiven Zerfall ist 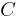 die Menge der am Anfang vorhandenen Radioaktivität. Wir nennen sie
die Menge der am Anfang vorhandenen Radioaktivität. Wir nennen sie 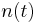 .
. 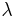 heißt Zerfallskonstante (siehe http://www.mathe-online.at/mathint/log/i.html#Zerfallskonstante). Jetzt kann gefragt werden, nach welcher Zeit nur mehr die Hälfte übrig ist? Diese Frage lösen wir mit Hilfe der Exponentialgleichung
heißt Zerfallskonstante (siehe http://www.mathe-online.at/mathint/log/i.html#Zerfallskonstante). Jetzt kann gefragt werden, nach welcher Zeit nur mehr die Hälfte übrig ist? Diese Frage lösen wir mit Hilfe der Exponentialgleichung 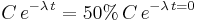 ,
,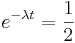
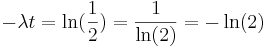 ,
,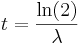
Welche ungeschickten Formulierungen wurden verwendet, welche Fehler wurden gemacht? Formuliert den Text so um, dass er das, was er sagen will, auf richtigere und schönere Weise zum Ausdruck bringt!
Text korrigieren: xxxThema
[Aufgabe für 2er- oder 3er-Gruppe] [Matthias]
xxx
Text korrigieren: Kurvendiskussion
[Aufgabe für 2er- oder 3er-Gruppe] [Jochen]
Auf einer Referatsseite im Internet wurde folgender Text gefunden. Lies ihn dir genau durch und korrigiere eventuelle Fehler bzw. Ungenauigkeiten!
Eine Kurvendiskussion besteht im Wesentlich aus 10 Teilaufgaben. Den Definitionsbereich kann man sehr einfach bestimmen, weil er immer R ist.
Um die Nullstellen berechnen zu können, löst man die Gleichung 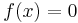 , weil eine Nullstelle immer der Schnittpunkt mit der x – Achse ist. Daher ist die Nullstelle immer N(0 / y).
Für eventuelle Extremstellen setzt man die 1. Ableitung Null. Der Grund ist recht einfach: die erste Ableitung gibt nämlich die mittlere Änderungsrate einer Funktion an. Will man zusätzlich entscheiden, ob es sich um einen Hoch- bzw. Tiefpunkt handelt, setzt man in die zweite Ableitung ein. Ist die zweite Ableitung größer als Null, dann handelt es sich um einen Hochpunkt, andernfalls um ein Minimum. Ist eine Funktion in einem bestimmten Intervall gegeben, dann kann es auch zu Extremstellen kommen, obwohl die 1. Ableitung ungleich Null ist. Den Unterschied zwischen lokalen und globalen Extremstellen habe ich nie verstanden. Ist eine Funktion streng monoton wachsend, so gilt:
, weil eine Nullstelle immer der Schnittpunkt mit der x – Achse ist. Daher ist die Nullstelle immer N(0 / y).
Für eventuelle Extremstellen setzt man die 1. Ableitung Null. Der Grund ist recht einfach: die erste Ableitung gibt nämlich die mittlere Änderungsrate einer Funktion an. Will man zusätzlich entscheiden, ob es sich um einen Hoch- bzw. Tiefpunkt handelt, setzt man in die zweite Ableitung ein. Ist die zweite Ableitung größer als Null, dann handelt es sich um einen Hochpunkt, andernfalls um ein Minimum. Ist eine Funktion in einem bestimmten Intervall gegeben, dann kann es auch zu Extremstellen kommen, obwohl die 1. Ableitung ungleich Null ist. Den Unterschied zwischen lokalen und globalen Extremstellen habe ich nie verstanden. Ist eine Funktion streng monoton wachsend, so gilt: 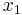 <
< 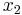 →
→ 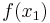
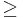
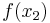
Mit der 1. Ableitung kann das Monotonieverhalten natürlich auch bestimmt werden. Ist 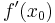 in einem bestimmten Intervall kleiner als Null, so ist die Funktion dort monoton fallend.
Nun zu den Wendepunkten: eine Wendestelle
in einem bestimmten Intervall kleiner als Null, so ist die Funktion dort monoton fallend.
Nun zu den Wendepunkten: eine Wendestelle 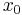 ist so definiert, dass sich die Krümmung an dieser Stelle nicht ändert. Deshalb muss man die 2. Ableitung bestimmen und die Gleichung
ist so definiert, dass sich die Krümmung an dieser Stelle nicht ändert. Deshalb muss man die 2. Ableitung bestimmen und die Gleichung 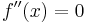 lösen. Zur Sicherheit – müsste man nicht – bildet man die 3. Ableitung und überprüft, dass
lösen. Zur Sicherheit – müsste man nicht – bildet man die 3. Ableitung und überprüft, dass 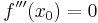 ungleich Null ist. Der Funktionsgraph der 1. Ableitung hat dort immer eine Extremstelle. Je nachdem, ob
ungleich Null ist. Der Funktionsgraph der 1. Ableitung hat dort immer eine Extremstelle. Je nachdem, ob 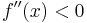 bzw.
bzw. 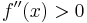 ist, spricht man von konkav bzw. konvex. Ein Sattelpunkt ist ein Wendepunkt mit waagrechter Tangente, d.h.
ist, spricht man von konkav bzw. konvex. Ein Sattelpunkt ist ein Wendepunkt mit waagrechter Tangente, d.h. 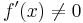 und
und 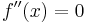 , weil es ja eine Wendestelle ist.
, weil es ja eine Wendestelle ist.
Ich hoffe, dass ich euch mit meinem Referat helfen konnte!
Verhalten von Funktionen
[Aufgabe für 2er- oder 3er-Gruppe] [Franz]
Gegeben sei eine Funktion 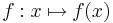 . Ist
. Ist 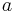 eine Konstante, so können aus
eine Konstante, so können aus 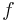 weitere Funktionen gewonnen werden:
weitere Funktionen gewonnen werden:
Diskutiert das Verhalten und die Graphen der Funktionen
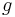 ,
, 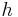 ,
, 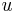 und
und 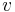 im Verhältnis zu jenen von
im Verhältnis zu jenen von 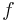 ! Gebt einige Beispiele an und erstellt aussagekräftige Grafiken!
! Gebt einige Beispiele an und erstellt aussagekräftige Grafiken!
Wie übertragen sich folgende Eigenschaften auf die Funktionen 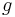 ,
, 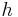 ,
, 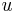 und
und 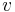 ?
?
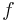 ist periodisch mit Periode
ist periodisch mit Periode 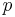 .
.
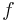 ist überall positiv.
ist überall positiv.
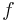 ist monoton steigend.
ist monoton steigend.
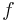 hat bei
hat bei 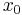 eine Nullstelle (d.h.
eine Nullstelle (d.h. 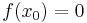 ).
).
Erstellt mit einem dynamischen Geometriesystem (z.B. GeoGebra) ein Arbeitsblatt, in dem anhand einer Funktion 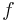 eurer Wahl die Konstante
eurer Wahl die Konstante 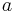 mittels eines Schiebereglers variiert werden kann!
mittels eines Schiebereglers variiert werden kann!
Das Integral
[Aufgabe für 2er-Gruppe] [Matthias]
Die zwei grundlegenden Interpretationen des Integrals lauten:
- Das Integral ist die Umkehroperation der Differentation. Jede mathematische Operation hat sein Spiegelbild. So wie die Paare Addition/Subtraktion, Multiplikation/Division, Potenzieren/Radizieren existiert das Paar Differentation/Integration.
Differentation: 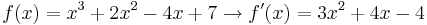
Integration: 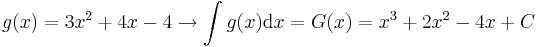
Die Funktionen 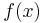 und
und 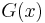 sind bis auf die Integrationskonstante
sind bis auf die Integrationskonstante 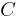 ident.
ident.
Diese Art von Integral nennt man unbestimmtes Integral. Das Ergebnis dieser Operation ist eine Funktion. Durch das Differenzieren geht jede Art von additiver Konstante verloren. Diese lässt sich durch die Integration nicht eindeutig wieder herstellen. Das Ergebnis der Integration ist daher eine Kurvenschar. Eine unendliche Anzahl von ähnlichen Funktionen, die entlang der y-Achse verschoben sind. Möchte man die Funktion genau bestimmen, ist ein Punkt notwendig, durch den die gesuchte Funktion geht.
- Das Integral dient zur Berechnung des Flächeninhaltes der Fläche unterhalb des Graphen einer Funktion.
Der Flächeninhalt einer Fläche entspricht einer Zahl. Diese Zahl lässt sich ebenfalls mit dem Integral berechnen. Dieses Integral wird bestimmtes Integral genannt. Zur Berechnung braucht man Informationen über die Ränder der zu berechnenden Fläche. Diese Ränder werden obere und untere Grenze genannt, diesesind mit den x-Koordinaten der Randpunkte ident.
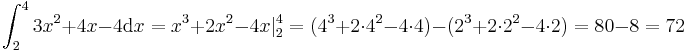 Flächeneinheiten.
Flächeneinheiten.
Aufgabe:
Überprüft, ob Differentation und Integration wirklich Umkehroperationen sind! Teilt die Funktionen auf. Jedes Gruppenmitglied leitet zwei Funktionen ab und integriert zwei andere. Dann werden die Ergebnisse verglichen und überprüft, ob sie übereinstimmen. Dabei gilt  und
und 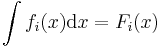 . Ist dies nicht der Fall, hat sich jemand verrechnet. Sucht und findet dabei gemachte Fehler!
. Ist dies nicht der Fall, hat sich jemand verrechnet. Sucht und findet dabei gemachte Fehler!
- Funktionen zur Differentation:
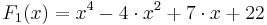 ,
, 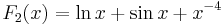 ,
, 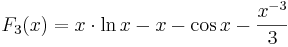 ,
, 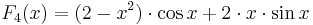
- Funktionen zur Integration:
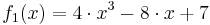 ,
, 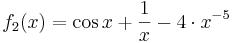 ,
, 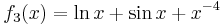 ,
, 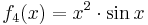
- Berechnet die bestimmten Intgrale von
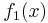 bis
bis 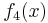 im Intervall
im Intervall 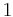 bis
bis 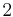 .
.
Lösungen der bestimmten Integrale:
-
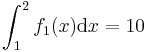 Flächeneinheiten (FE)
Flächeneinheiten (FE)
-
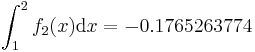 FE (Hier ist der Betrag zu nehmen.)
FE (Hier ist der Betrag zu nehmen.)
-
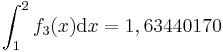 FE
FE
-
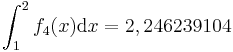 FE
FE
Kurvendiskussion
[Aufgabe für 2er- oder 3er-Gruppe] [Jochen]
- Erklärt die Berechnung der Nullstellen einer Funktion. Achtet dabei auf die mögliche Anzahl der Lösungen!
- Erklärt die Berechnung der Extremstellen einer Funktion!
- Wie lässt sich zwischen Hoch- und Tiefpunkt unterscheiden?
- Worin besteht der Unterschied zwischen lokalen und globalen Extremstellen?
- Erklärt die Berechnung der Wendestellen einer Funktion!
- Wann spricht man von einem Sattelpunkt?
- Wie kann man bei einer Funktion die Eigenschaften Monotonie und Krümmung untersuchen?
Erstellt mit einem dynamischen Geometrieprogramm (z.B. GeoGebra) ein Arbeitsblatt, das die Zusammenhänge der ersten drei Ableitungen zeigt!
Bewegung (fächerübergreifend mit Physik)
[Aufgabe für 2er- oder 3er-Gruppe] [Franz]
Was haben Zeit, Weg (Ort), Geschwindigkeit und Beschleunigung mit dem Differenzieren und Integrieren zu tun? Ihr könnt dabei davon ausgehen, dass eine Bewegungsform durch eine Zuordnung
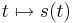
beschrieben wird. Dabei ist 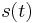 der Ort des betrachteten Objekts zur Zeit
der Ort des betrachteten Objekts zur Zeit 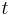 .
.
Gebt einige Beispiele für Bewegungsformen an und erstellt aussagekräftige Grafiken oder Animationen (etwa mit einem Computeralgebra-System).
Beantwortet folgende Fragen:
- Kann die Geschwindigkeit als Funktion der Zeit erhalten werden, wenn der Ort als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Kann die Beschleunigung als Funktion der Zeit erhalten werden, wenn der Ort als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Kann die Beschleunigung als Funktion der Zeit erhalten werden, wenn die Geschwindigkeit als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Kann der Ort als Funktion der Zeit erhalten werden, wenn die Geschwindigkeit als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Kann der Ort als Funktion der Zeit erhalten werden, wenn die Beschleunigung als Funktion der Zeit bekannt ist? Wenn ja, wie?
- Wie kann der Ort als Funktion der Zeit erhalten werden, wenn bekannt ist, dass die Beschleunigung konstant (
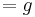 ) ist, und dass zur Zeit
) ist, und dass zur Zeit 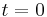 sowohl der Ort als auch die Geschwindigkeit gleich 0 sind? (Kommt euch das Ergebnis bekannt vor?)
sowohl der Ort als auch die Geschwindigkeit gleich 0 sind? (Kommt euch das Ergebnis bekannt vor?)
Kosten- und Preistheorie
[Aufgabe für 2er- oder 3er-Gruppe] [Peter]
Stichworte: Betriebsoptimale Menge, Carnotscher Punkt.
Funktionstypen
[Aufgabe für 2er- oder 3er-Gruppe] [Matthias] Eine klassische Aufgabe in der Schule ist in Österreich eine Kurvendiskussion. Dabei werden die Eigenschaften von Funktionen untersucht. Die zu untersuchenden Funktionen kommen aus den unterschiedlichen Bereichen der Wissenschaft, sehen verschieden aus und besitzen daher auch klassizifierbare Eigenschaften.
Eine Kurvendiskussion besteht aus Punkten, die oft unterschiedlich gruppiert werden, aber im Prinzip dasselbe darstellen.
Übersicht über Funktioneneigenschaften
Stichworte: Welche Typen von Funktionen gibt es, was sind ihre charakteristischen Eigenschaften? Die Beschreibung soll folgende Begriffe enthalten:
- Asymptoten
- Definitionsmenge
- exponential-
- logarithmisch
- periodisch
- Polstelle
- Polynom
- Symmetrie, symmetrisch
- Winkelfunktion
- Wurzel