Potenzfunktionen - Einführung: Unterschied zwischen den Versionen

Version vom 8. Dezember 2008, 16:45 Uhr

Einführung

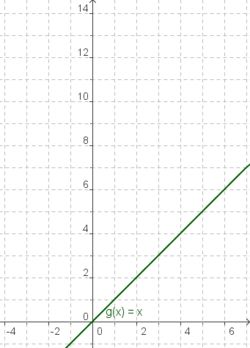
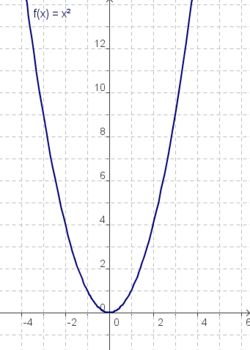
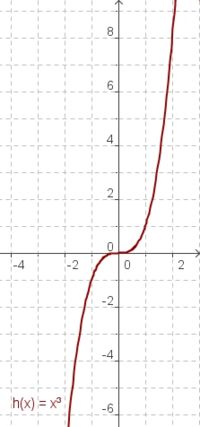
Die Funktionen x, x² und x³

g(x) = x		f(x) = x²		h(x) = x³

Aufgabe 1  Vergleiche den Graph der Funktion mit h(x) = x3 mit dem Graphen der Funktion g(x) = x. Beschreibe Gemeinsamkeiten und Unterschiede! Vergleiche den Graph der Funktion mit h(x) = x3 mit dem Graphen der quadratischen Funktion mit f(x) = x2. Beschreibe Gemeinsamkeiten und Unterschiede!

Die Graphen und ein Wanderer

Aufgabe 2  Ein Wanderer geht legt bei seinem Weg von A nach B einen Höhenunterschied von 10 m zurück. Wir betrachten nun drei verschiedene Formen des Verbindungsweges. Diese drei Wege haben im Seitenprofil in etwa die eingezeichneten Formen W1, W2, W3. Beschreibe den Wanderweg jeweils entlang dieser drei Wege, den der Wanderer zurücklegt, wenn er von A nach B geht.

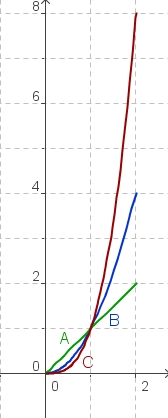
Wir betrachten jetzt die drei Funktionen mit ihren Graphen:

im Bereich von x = 0 bis x = 2.

Aufgabe 3  Begründe mit Hilfe der Tabelle, warum die Graphen A und B in der Umgebung des Nullpunktes stärker steigen als der Graph C. Ab welchem Punkt steigt der Graph stärker als der Graph A? Ab welchem Punkt steigt der Graph stärker als der Graph B?

{{Arbeiten|NUMMER=4|ARBEIT= Betätige den Schieberegler

Teste Dein Wissen

Ordne die Funktionsterme den Funktionsgraphen zu!

weitere Tests