Einfluss von c: Unterschied zwischen den Versionen
(→Einfluss von c: Vorlage Video eingefügt) |
(→Einfluss von c: Reihenfolge geändert) |
||
| Zeile 45: | Zeile 45: | ||
{| | {| | ||
| | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{Arbeiten|NUMMER=C2|ARBEIT= | {{Arbeiten|NUMMER=C2|ARBEIT= | ||
| − | + | Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen! | |
| − | + | ||
| − | + | ||
}} | }} | ||
||{{#ev:youtube|mSgduUqD_RE|150}} | ||{{#ev:youtube|mSgduUqD_RE|150}} | ||
| Zeile 59: | Zeile 53: | ||
---- | ---- | ||
| + | |||
{| | {| | ||
| | | | ||
| + | Nun betrachten wir den Einfluss von <math> \ c </math> in | ||
| + | |||
| + | :<math> x \rightarrow \cos ( x + c ) </math>. | ||
| + | |||
{{Arbeiten|NUMMER=C3|ARBEIT= | {{Arbeiten|NUMMER=C3|ARBEIT= | ||
| − | + | <ggb_applet height="50" width="150" type="button" filename="cos_c.ggb" /> <br> | |
| + | |||
| + | Öffne dieses GeoGebra-Applet und bearbeite damit obige Aufgaben eins bis vier nochmals. | ||
}} | }} | ||
||{{#ev:youtube|mSgduUqD_RE|150}} | ||{{#ev:youtube|mSgduUqD_RE|150}} | ||
|} | |} | ||
| + | |||
---- | ---- | ||
| Zeile 95: | Zeile 97: | ||
''Lösung zu Aufgabe C''2: {{versteckt| | ''Lösung zu Aufgabe C''2: {{versteckt| | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Eine mögliche Begründung: | Eine mögliche Begründung: | ||
| Zeile 110: | Zeile 106: | ||
Die Bestimmung der Nullstellen von <math> x \rightarrow \sin ( x + c ) </math> und Vergleich mit den Nullstellen der Sinuskurve zeigt, dass jeder Funktionswert für <math>\ c > 0 </math> bereits ein Stück weiter links angenommen wird. Genauer, der Graph wird also für <math>\ c > 0</math> um <math>\ c </math> nach links verschoben und für <math>\ c < 0 </math> entsprechend nach rechts. | Die Bestimmung der Nullstellen von <math> x \rightarrow \sin ( x + c ) </math> und Vergleich mit den Nullstellen der Sinuskurve zeigt, dass jeder Funktionswert für <math>\ c > 0 </math> bereits ein Stück weiter links angenommen wird. Genauer, der Graph wird also für <math>\ c > 0</math> um <math>\ c </math> nach links verschoben und für <math>\ c < 0 </math> entsprechend nach rechts. | ||
| + | }} | ||
| + | |||
| + | ''Lösung zu Aufgabe C''3: {{versteckt| | ||
| + | Die allgemeine Kosinusfunktion verhält sich bei Variation von <math> \ c </math> genauso wie die allgemeine Sinusfunktion. | ||
| + | |||
| + | [[Bild:N_cos_c.jpg|center]] | ||
}} | }} | ||
Version vom 12. Februar 2009, 21:34 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Einfluss von c
|
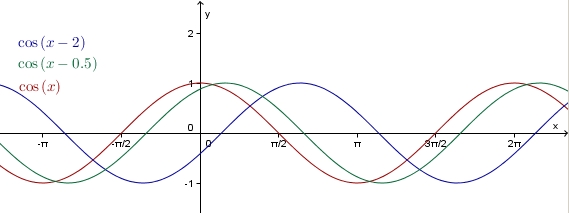
Wir betrachten nun den Einfluss von
|
|
|
Nun betrachten wir den Einfluss von
|
Lösung zu Aufgabe C1:
Lösung zu Aufgabe C2:
Eine mögliche Begründung:
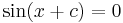
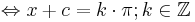
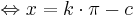
Die Bestimmung der Nullstellen von 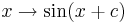 und Vergleich mit den Nullstellen der Sinuskurve zeigt, dass jeder Funktionswert für
und Vergleich mit den Nullstellen der Sinuskurve zeigt, dass jeder Funktionswert für 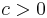 bereits ein Stück weiter links angenommen wird. Genauer, der Graph wird also für
bereits ein Stück weiter links angenommen wird. Genauer, der Graph wird also für 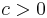 um
um  nach links verschoben und für
nach links verschoben und für 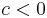 entsprechend nach rechts.
entsprechend nach rechts.
Lösung zu Aufgabe C3:
Die allgemeine Kosinusfunktion verhält sich bei Variation von  genauso wie die allgemeine Sinusfunktion.
genauso wie die allgemeine Sinusfunktion.
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe C1 ein Hefteintrag "versteckt" ist!
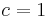 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 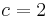 und
und 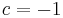 , sowie
, sowie 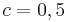 und
und 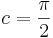 auf den Graphen auswirken und überprüfe deine Vermutung.
auf den Graphen auswirken und überprüfe deine Vermutung. 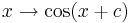 .
.