Potenzfunktionen - Einführung: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
K (→Teste Dein Wissen) |
(-Autoren (am ende und Anfang)) |
||
| Zeile 85: | Zeile 85: | ||
[http://hotpotatoes.bildung-rp.de/parabel.htm Wähle den zum Graphen passenden Funktionsterm aus!] | [http://hotpotatoes.bildung-rp.de/parabel.htm Wähle den zum Graphen passenden Funktionsterm aus!] | ||
| − | |||
| − | |||
| − | |||
Version vom 20. April 2009, 08:09 Uhr
Inhaltsverzeichnis |
Einführung
Die Graphen der Funktionen x, x² und x³
Die Graphen und ein Wanderer
|
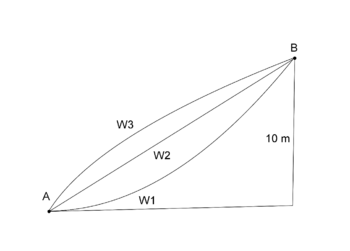
|
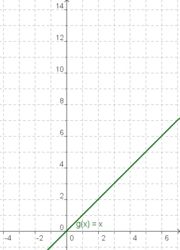
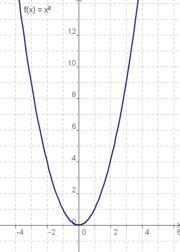
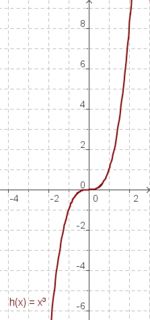
Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2
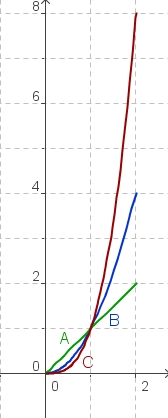 |
g(x) = x (Graph A) f(x) = x2 (Graph B) | |||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
|
Verändern von Variablen
Der Graph der Funktion ha(x)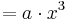
|
Der Graph der Funktion ha,c(x)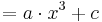
|
Teste Dein Wissen
Ordne die Funktionsterme den Funktionsgraphen zu! (auf www.mathe-online.at)
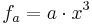 in Abhängigkeit von a!
in Abhängigkeit von a!

