Quadratische Funktionen 2: Unterschied zwischen den Versionen
| Zeile 112: | Zeile 112: | ||
{{#ev:youtube|BeXmLxAicPg|150}} | {{#ev:youtube|BeXmLxAicPg|150}} | ||
| + | '''!!!!!ab hier geht es los!!!!!!''' | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
Version vom 4. Juli 2011, 11:43 Uhr
!!!!!Dieser Lernpfad wird gerade überarbeitet!!!!!!
Quadratische Funktionen
erstellt von
Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann (2009)
Überarbeitet von Silvia Joachim und Karl Haberl (2011)
im Rahmen eines internationalen Projektes von
Medienvielfalt im Mathematikunterricht
Du erwirbst / stärkst in diesem Lernpfad folgende Kompetenzen.
Informationen zum Einsatz des Lernpfads im Unterricht: Didaktischer Kommentar

!!!!!!ab hier löschen!!!!!!!
Ideensammlung:
Jungs:
Feuerwehr
Brücken
Luftwiederstand
Kraftstoffverbrauch
senkrechter Wurf
Tunnel
Mädels:
Springreiten
Eiskunstlauf
Lernvideo
!!!!!ab hier geht es los!!!!!!
Quick-Links:
- Für LehrerInnen: Didaktischer Kommentar
- Wiederholung: Erfahre hier die Eigenschaften der Quadratfunktionen und der Normalparabel!
- Wiederholung: Einfluss der Parameter bei linearen Funktionen
- FAQ: Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
- Station 1: Erforsche hier den Einfluss der Parameter auf das Aussehen des Graphen!
- Station 2: Erfahre hier, wie du aus dem Graphen einer Funktion deren Term ablesen kannst - und mehr!
- Anwendungen: Lerne hier einige Anwendungen kennen!
 |
Hallo! Wäre es nicht toll, wenn du hellsehen könntest? Wenn du den Graphen eines Funktionsterms auch ohne Wertetabelle direkt zeichnen könntest? Wenn du aus dem Graphen einer Funktion deren Term ablesen könntest? Für die linearen beherrschst du diese Kunst wahrscheinlich schon. Dann wirst du vieles von deinem Wissen auf die allgemeine quadratische Funktion übertragen können. |
|
Hinweise:
|
|
Dieser Lernpfad enthält zwei Stationen, die du am besten nacheinander bearbeitest. Klicke dazu einfach auf die gewünschte Station! Wenn du vorher die Eigenschaften der Quadratfunktion und der Normalparabel wiederholen möchtest, dann sehe dir dieses Video an.
<graphviz> digraph G { rankdir=RL; "Term" -> "Graph"[label=" "]; edge [color = white]; "Term" -> "Hellsehen"; "Hellsehen" -> "Graph"; edge [color = black]; rankdir=LR; "Graph" -> "Term"; } </graphviz> Anwendungen |
|
Experimentier-Ecke
|
|
Nun hast du es wirklich geschafft und den ganzen Lernpfad bearbeitet. Du kannst stolz sein - gut gemacht! Hefteintrag: Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alles Wichtige notiert hast! Ich wünsche dir noch einen schönen Tag! |
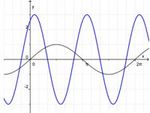

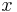 -Achse mit Vielfachen von
-Achse mit Vielfachen von 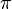 beschriftet. Indem man die
beschriftet. Indem man die 
