Pool 1: Unterschied zwischen den Versionen
(→Analyse des Verhaltens einer gegebenen Funktion) |
|||
| Zeile 31: | Zeile 31: | ||
<font color="#004400">[Aufgabe für 2er-Gruppe]</font> [Franz] | <font color="#004400">[Aufgabe für 2er-Gruppe]</font> [Franz] | ||
| − | + | Die Funktion | |
<center><math>\gamma(v)=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}</math></center> | <center><math>\gamma(v)=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}</math></center> | ||
| − | für Geschwindigkeiten <math>v</math>, die | + | spielt in der Relativitätstheorie eine wichtige Rolle. Die Variable <math>v</math> |
| + | steht für die Geschwindigkeit eines Körpers, die Konstante <math>c</math> bezeichnet die Lichtgeschwindigkeit. | ||
| + | Wie ... für Geschwindigkeiten <math>v</math>, die | ||
*sehr viel kleiner als die Lichtgeschwindigkeit <math>c</math> | *sehr viel kleiner als die Lichtgeschwindigkeit <math>c</math> | ||
*sehr nahe der Lichtgeschwindigkeit <math>c</math> | *sehr nahe der Lichtgeschwindigkeit <math>c</math> | ||
Version vom 14. September 2008, 13:25 Uhr
Lernpfad zur Schnittstelle Sekundarstufe 2 - Universität
Aufgabenpool 1
Startseite des Lernpfads | Aufgabenpool 2 | Didaktischer Kommentar
Inhaltsverzeichnis |
Differentialgleichung versus Differenzengleichung
[Aufgabe für 2er-Gruppe] [Walter]
Stichworte: Ein Problem, das sowohl mit DGL als auch mit Differenzengleichung gelöst werden kann. Beide Partner arbeiten zuerst selbständig, führen dann ihre Ergebnisse zusammen und diskutieren sie.
Integrationsverfahren vergleichen
[Aufgabe für xxxer-Gruppe] [Matthias]
Stichworte: analytische / näherungsweise mit Taylorpolynomen / näherungsweise numerisch. Mögliche Tools: CAS, Tabellenkalkulation.
Logistische Abbildung
[Aufgabe für 2er-Gruppe] [Matthias]
Stichworte: Verschiedene Aufgaben für verschiedene Parameter- und Anfangswerte (manche oszillierend, manche chaotisch), visualisieren! Dann die Ergebnisse zusammenführen und beschreiben, dass/wie das Verhalten vom Parameter abhängt. Mögliche Tools: CAS, Tabellenkalkulation.
Analyse des Verhaltens einer gegebenen Funktion
[Aufgabe für 2er-Gruppe] [Franz]
Die Funktion
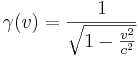
spielt in der Relativitätstheorie eine wichtige Rolle. Die Variable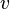 
steht für die Geschwindigkeit eines Körpers, die Konstante 
bezeichnet die Lichtgeschwindigkeit.
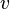Wie ... für Geschwindigkeiten , die
- sehr viel kleiner als die Lichtgeschwindigkeit
- sehr nahe der Lichtgeschwindigkeit
sind? Stelle insbesondere Näherungsformeln für die beiden Grenzfälle auf! Benutze die dir bekannten Methoden zur Analyse einer Funktion, wie
- Plotten des Funktionsgraphen (überlege, wie du dabei mit der Konstanten umgehst und welchen Bereich für 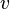du wählst!) und elementare Analyse des Funktionsterms, um das Aussehen des Graphen qualitativ zu erklären,
- Methoden der Kurvendiskussion (Definitionsmenge, Nullstellen, Extremstellen, Wendestellen,... ermitteln) und
- Reihenentwicklung bzw. verwandte Näherungsmethoden.
Anmerkung: Die Funktiontritt in vielen Beziehungen der speziellen Relativitätstheorie auf. So stellt sie beispielweise den Faktor dar, um den bewegte Uhren langsamer gehen als ruhende, und um den Objekte in Bewegungsrichtung verkürzt sind. Im Zwillingsparadoxon gibt sie den Faktor an, um den die von den Zwillingen gemessenen Zeinintervalle voneinander abweichen. Die berühmte Beziehung
verallgemeinert sich für einen bewegten Körper zu
.
Ergänzungsaufgabe (fächerübergreifend mit Physik): Diskutiere die von dir erhaltenen Ergebnisse physikalisch! Tool: CAS
Epidemie
[Aufgabe für xxxer-Gruppe] [Peter]
xxx
Elastizität
[Aufgabe für xxxer-Gruppe] [Peter]
xxx
Zentralmaße vergleichen
[Aufgabe für xxxer-Gruppe] [Walter, mgl.weise Josef]
xxx
Streuungsmaße vergleichen
[Aufgabe für xxxer-Gruppe] [Walter, mgl.weise Josef]
xxx
Rekursionsverfahren vergleichen
[Aufgabe für xxxer-Gruppe] [Walter, mgl.weise Josef]
xxx
