Lösung einfacher Differentialgleichungen: Unterschied zwischen den Versionen
| Zeile 65: | Zeile 65: | ||
| − | [[Diskret - kontinuierlich|Zurück zum Lernpfad]] | + | [[Diskret - kontinuierlich#L.C3.B6sung_einfacher_Differentialgleichungen|Zurück zum Lernpfad]] |
Version vom 23. August 2011, 11:29 Uhr
Eine grundlegende Variante zur Lösung von Differentialgleichungen (DGLG) wird Seperation der Variablen (Trennung der Variablen) genannt. Bei dieser Vorgehensweise muss Du die DGLG so umformen, dass sich auf den beiden Seiten der Gleichung nur gleiche Variablen befinden, das heißt, zum Beispiel alle Terme mit  auf die rechte Seite und alle Terme mit
auf die rechte Seite und alle Terme mit 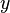 auf die linke Seite der Gleichunge zu bringen.
Statt der Ableitung
auf die linke Seite der Gleichunge zu bringen.
Statt der Ableitung 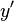 schreibt man
schreibt man 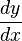 (sprich d y nach d x ). Bei diesem Ausruck handelt es sich zwar um keinen Bruch, Du darfst ihn aber aus mathematischer Sich wie einen behandeln, damit Du die Variablen trennen kannst.
Da das Ergebnis einer DGLG ja eine Kurvenschar ist, kannst Du durch die Angabe einer Anfangsbedingung eine eindeutige Funktion bestimmen, Dir die Integrationskonstante
(sprich d y nach d x ). Bei diesem Ausruck handelt es sich zwar um keinen Bruch, Du darfst ihn aber aus mathematischer Sich wie einen behandeln, damit Du die Variablen trennen kannst.
Da das Ergebnis einer DGLG ja eine Kurvenschar ist, kannst Du durch die Angabe einer Anfangsbedingung eine eindeutige Funktion bestimmen, Dir die Integrationskonstante 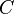 ausrechnen.
ausrechnen.
|
Löse die Differenzialgleichung |
Lösung der Aufgabe 1:
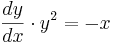
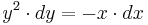
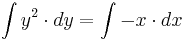
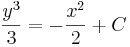
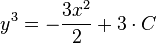
allgemeine Lösung: ![y=\sqrt[3]{-\frac{3x^2}{2}+3 \cdot C}](/images/math/8/a/2/8a21d3a70ff94bc887d1b47eacbab1c5.png)
Einsetzen der Anfangsbedingung:
![2=\sqrt[3]{-\frac{3\cdot 2^2}{2}+3 \cdot C}](/images/math/8/a/4/8a45d598b5f8318cfd824eda196b550a.png)
![2=\sqrt[3]{-6+3 \cdot C}](/images/math/d/b/0/db0bd337e045d5de0b28808ddda12d98.png)
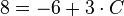
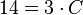
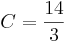
spezielle Lösung mit gegebener Anfangsbedingung: ![y=\sqrt[3]{-\frac{3x^2}{2}+14}](/images/math/0/2/d/02d52a342a9ed150359962a66a519e6b.png)
|
Löse die Differenzialgleichung |
Lösung der Aufgabe 2:
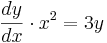
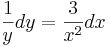
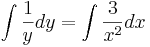
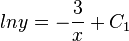
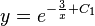
allgemeine Lösung: 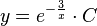
Einsetzen der Anfangsbedingung:
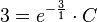
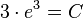
spezielle Lösung mit gegebener Anfangsbedingung: 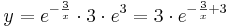
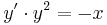 mit der Anfangsbedingung
mit der Anfangsbedingung 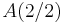 !
!
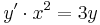 mit der Anfangsbedingung
mit der Anfangsbedingung 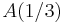 !
!

