Wurzelfunktionen Eigenschaften: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 7: | Zeile 7: | ||
* Er ermöglicht die Berechnung des''' Steigungswinkels'''. | * Er ermöglicht die Berechnung des''' Steigungswinkels'''. | ||
* Er gibt die '''mittlere Änderungsrate''' an. | * Er gibt die '''mittlere Änderungsrate''' an. | ||
| + | <br> | ||
| + | <br> | ||
| + | {{Arbeiten| | ||
| + | NUMMER=5| ARBEIT= | ||
| + | Zeichne den Graphen der Funktionen <math>f:x \rightarrow x^2</math> im Intervall [0;3] und den Graphen der Funktion <math> g:x \rightarrow \sqrt x</math> im Intervall [0;7] in ein Koordinatensystem. | ||
| + | |||
| + | Beschreibe mit Worten die besondere Lage dieser beiden Graphen zueinander. | ||
| + | }} | ||
Version vom 11. Mai 2012, 07:50 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Der Differenzenquotient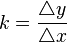 
= 
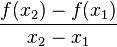ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x.
- Er gibt die Steigung einer Sekante durch die Punkte
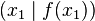und 
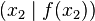
- Er ermöglicht die Berechnung des Steigungswinkels.
- Er gibt die mittlere Änderungsrate an.
Aufgabe 5
Zeichne den Graphen der Funktionen Beschreibe mit Worten die besondere Lage dieser beiden Graphen zueinander. |
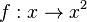im Intervall [0;3] und den Graphen der Funktion 
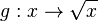im Intervall [0;7] in ein Koordinatensystem.
