Wurzelfunktionen Eigenschaften: Unterschied zwischen den Versionen
| Zeile 35: | Zeile 35: | ||
Gib für die folgenden zwei funktionalen Abhängigkeiten | Gib für die folgenden zwei funktionalen Abhängigkeiten | ||
| − | # die Funktionsgleichung an und | + | # die Funktionsgleichung an, erstelle eine Wertetabelle und zeichne den Graphen der beiden Funktionen! |
| − | + | # Gib die mittlere Änderungsrate für beide Funktionen im Intervall <math>\left[ 2; 3\right]</math> an! | |
| + | # Halte schriftlich fest, welche Bedeutung die mittlere Änderungsrate in diesem Zusammenhang hat! | ||
<br> | <br> | ||
a) Dem Oberflächeninhalt <math>A = 36</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | a) Dem Oberflächeninhalt <math>A = 36</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
b) Dem Volumen <math>V = 16</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | b) Dem Volumen <math>V = 16</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
}} | }} | ||
Version vom 11. Mai 2012, 08:16 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Der Differenzenquotient 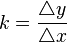 =
= 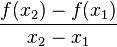 ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x.
ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x.
- Er gibt die Steigung einer Sekante durch die Punkte
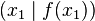 und
und 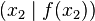
- Er ermöglicht die Berechnung des Steigungswinkels.
- Er gibt die mittlere Änderungsrate an.
|
Zeichne den Graphen der Funktionen Gib den Steigungswinkel der Sekante an!
|
|
Gib für die folgenden zwei funktionalen Abhängigkeiten
|
|
Gib für die folgenden zwei funktionalen Abhängigkeiten
|
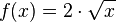 und ermittle die Steigung der Sekante durch die Punkte
und ermittle die Steigung der Sekante durch die Punkte 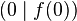 und
und 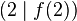 !
!
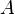 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius  zugeordnet.
zugeordnet.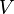 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius ![\left[ 2; 3\right]](/images/math/e/3/1/e312e90f1b43263f576d2f38125b503e.png) an!
an!
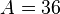 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius 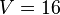 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius 
