Bestimmung der Funktionsgleichung aus dem Graphen
Einführung - Station 1: Einfluss der Parameter - Station 2: Bestimmung der Funktionsgleichung und mehr - Station 3: Anwendungen in der Physik - Station 4: Zusatzaufgaben
Inhaltsverzeichnis |
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Informationen aus dem Graphen
|
|
|
Bestimmung einer Funktionsgleichung aus dem Graphen
Beachte, zu einem Graphen kann es mehrere zugehörige Funktionsgleichungen geben. D.h. die Antwort auf die Frage nach einer Funktionsgleichung zu einem gegebenen Graphen muss nicht immer eindeutig sein.
|
Um zu sehen wie man aus dem Graphen einer Funktion eine zugehörige Funktionsgleichung bestimmen kann, klicke in die leeren Kontrollkästchen. |
|
Bestimme zu folgenden Graphen je eine zugehörige Funktionsgleichung der Form |
Jetzt noch was zum Knobeln!!!
|
Lösung zu Aufgabe 1:
Amplitude: 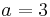
Wertemenge: ![W = [-3;\ 3]](/images/math/7/f/4/7f4a584468ac15313bbdcbd41602ca3e.png)
Periode: 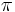
Nullstellen: 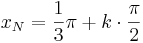 mit
mit  oder
oder 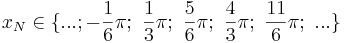
Tiefpunkte: 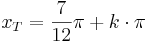 mit
mit  oder
oder 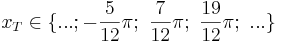
Hochpunkte: 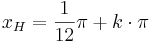 mit
mit  oder
oder 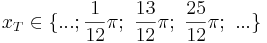
streng monoton fallend: ![...;\ [\frac{1}{12}\pi;\ \frac{7}{12}\pi];\ [\frac{13}{12}\pi;\ \frac{19}{12}\pi];\ ...](/images/math/2/3/5/2352ffad5112a215b1551af34791f362.png)
![...;\ [-\frac{5}{12}\pi;\ \frac{1}{12}\pi];\ [\frac{7}{12}\pi;\ \frac{13}{12}\pi];\ [\frac{19}{12}\pi;\ \frac{25}{12}\pi];\ ...](/images/math/a/b/3/ab3f03ffd65ea28a0ffd4a78e3cd5295.png)
Lösung zu Aufgabe 3: Hier kannst Du überprüfen, ob deine Ergebnisse stimmen. Stelle dazu die Schieberegler entsprechend ein.
Lösung zu Aufgabe 4:
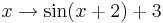 und
und 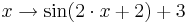
Super! Nun hast du es geschafft und das Ende des Lernpfades erreicht.
Hefteintrag: Lese dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast.
Nun hast du es wirklich geschafft. Du kannst stolz sein - gut gemacht! Ich wünsche dir noch einen schönen Tag!
Experimentier-Ecke
|
Du hast doch bestimmt einen Zirkel, oder? Genauer gesagt benötigst du nicht den Zirkel, sondern nur die Bleistiftmine für dieses Experiment. Die Mine sollte schräg angefeilt sein. Nimm die Mine aus dem Zirkel und lege sie auf ein Blatt Papier. Wenn du die Mine nun mit einem leichten Druck über das Papier rollst, kannst du den Graphen einer Sinusfunktion erkennen. Diesen kannst du dann gerne noch mit einem Stift nachfahren. |
Weiter geht es mit
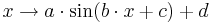 .
.

