Anwendungen in der Physik
Einführung - Station 1: Einfluss der Parameter - Station 2: Bestimmung der Funktionsgleichung und mehr - Station 3: Anwendungen in der Physik - Station 4: Zusatzaufgaben
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Anwendungen in der Physik
|
Die Möve hängt an einer Feder und schwingt bei einmaliger Auslenkung. Im Bild sind die Ruhelage und die größten Auslenkungen aus dieser zu sehen. Die Zeitabstände zwischen den einzelnen Fotos sind jeweils gleich groß.
|
|
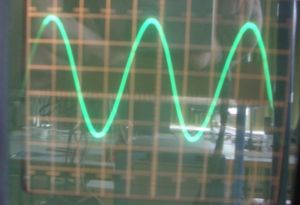
Auf einem Oszilloskop sieht man obiges Bild.
|
a) Die Sinuskurve ist um 0,75 nach oben verschoben.
Der Abstand zwischen Hoch- und Tiefpunkt der Sinuslinie ist 4,5, also ist die Amplitude 2,25.
Die Periodendauer ist 3,75.
Die Sinuskurve fängt mit 0,25 am linken Rand an.
b) Es sind d = 0,75, a = 2,25, b = 2*PI/3,75 und c = -0,224.|
Die Abbildung zeigt dir, wie man die Bewegung eines schwingenden Objekts mit Hilfe eines Streifen Papier, der an ihm gleichmäßig vorbei entlanggezogen wird, "festhalten kann". Auf diese Weise kann die Auslenkung als Funktion der Zeit aufgezeichnet werden. Nach diesem Prinzip können beispielsweise die Schwingungen, die ein Erdbeben auslöst, protokolliert werden. |
|
Diese Abbildung zeigt ein solches "Protokoll". a.) Wie viele Einzelschwingungen führt das Objekt pro Sekunde aus? (Diese Zahl gibt die "Frequenz" an - wenn beispielsweise 100 Einzelschwingungen pro Sekunde stattfinden, so sagt man, die Schwingung hat eine Frequenz von 100 Hertz und schreibt f = 100 Hz. Unter "einer Einzelschwingung" ist dabei ein vollständiges Duchlaufen einer Periode - ein "hin und her" gemeint). b.) Stelle die Funktionsgleichung der Schwingung auf! |
|
Weiter geht es mit
 an!
an!