FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Anwendungen in der Physik
Hefteintrag: Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben!
Es gibt viele periodische Vorgänge, also Vorgänge die sich nach einer bestimmten Zeit wiederholen. Zeichnet man deren zeitlichen Verlauf auf, so erhält man einen sinusförmigen Graph.
| :
|
Aufgabe P2 - Das Fadenpendel 
- Beschreibe das Experiment und verwende dabei die passenden mathematischen und physikalischen Fachbegriffe!
- Betrachte den Graphen und überlege dir, inwiefern er nur fast der Graph einer Sinusfunktion ist!
- Diskutiere was an dem Exerperiment "schief" gelaufen sein könnte!
|
|
|
|
Aufgabe P3 - Das Oszilloskop 
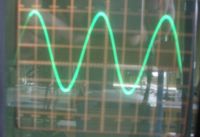
Ein Oszilloskop (umgangssprachlich "Oszi") ist ein elektronisches Messgerät mit dessen Hilfe u.a. der Verlauf der Spannung zeitlich dargestellt werden kann. Auf einem Oszilloskop sieht man dieses Bild. Dabei ist die x-Ablenkung auf 0,1ms/div (Millisekunden pro Teilung) und die y-Ablenkung auf 1V/div (Volt pro Teilung) eingestellt.
- Gib die Spitzenspannung (Amplitude) an!
- Wie groß ist die Schwingungsdauer?
- Bestimme die Frequenz!
|
|
Möchtest Du genaueres über das Oszilloskop wissen? Dann kannst Du Dich hier freiwillig informieren.
|
|
Aufgabe P4 - Erdbeben 
Die Abbildung zeigt dir, wie man die Bewegung eines schwingenden Objekts mit Hilfe eines Streifen Papier, der an ihm gleichmäßig vorbei entlanggezogen wird, "festhalten kann".
Auf diese Weise kann die Auslenkung als Funktion der Zeit aufgezeichnet werden. Nach diesem Prinzip können beispielsweise die Schwingungen, die ein Erdbeben auslöst, protokolliert werden.
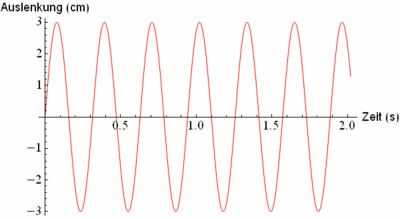
Die folgende Abbildung zeigt ein solches "Protokoll".
- Wie viele Einzelschwingungen führt das Objekt pro Sekunde aus? Tipp: [Anzeigen][Verstecken]
- Diese Zahl gibt die "Frequenz" an, wenn beispielsweise 100 Einzelschwingungen pro Sekunde stattfinden, so sagt man, die Schwingung hat eine Frequenz von 100 Hertz und schreibt
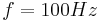 . Unter "einer Einzelschwingung" ist dabei ein vollständiges Duchlaufen einer Periode, ein "hin und her" gemeint. . Unter "einer Einzelschwingung" ist dabei ein vollständiges Duchlaufen einer Periode, ein "hin und her" gemeint.
- Stelle die Funktionsgleichung der Schwingung auf!
|
|
Aufgabe P5 
- In dem Applet auf diesem Arbeitsblatt werden die Parameter einer Sinusschwingung aus der Physik behandelt. Bearbeite die dort gestellten Aufgaben!
- In diesem Lernpfad zur harmonischen Schwingung findest du als Lernschritt 8 eine Aufgabe. Kannst du sie lösen? Fertige eine Zeichnung an!
|
Lösung zu Aufgabe P 1: [Anzeigen][Verstecken]
Lösung zu Aufgabe P 3: [Anzeigen][Verstecken]
1. Die Spitzenspannung (Amplitude) beträgt ungefähr 2,3V.
2. Die Schwinungsdauer beträgt in etwa 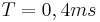 .
.
3. Es gibt mehrere Möglichkeiten die Frequenz zu bestimmen. So errechnet man z.B. aus der Schwingungsdauer, dass 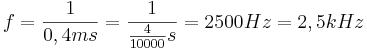 gilt.
gilt.
Nun hast du es wirklich geschafft und den ganzen Lernpfad bearbeitet. Du kannst stolz sein - gut gemacht!
Hefteintrag: Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alles Wichtige notiert hast!
Ich wünsche dir noch einen schönen Tag!
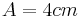
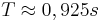
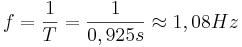
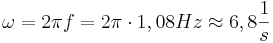 oder
oder 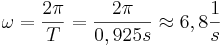
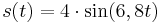
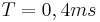 .
.
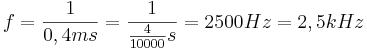 gilt.
gilt.
 !
!
 ?
?
 !
!
 !
!
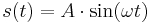 an!
an!

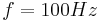 . Unter "einer Einzelschwingung" ist dabei ein vollständiges Duchlaufen einer Periode, ein "hin und her" gemeint.
. Unter "einer Einzelschwingung" ist dabei ein vollständiges Duchlaufen einer Periode, ein "hin und her" gemeint.

