FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Hefteintrag: Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben!
Informationen aus dem Graphen
|
Aufgabe 1 
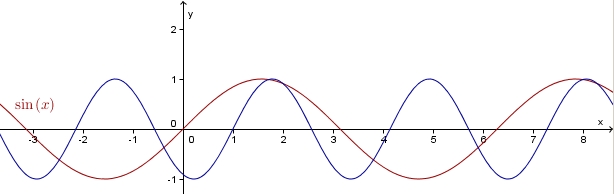
Auf diesem Bild ist ein Graph einer allgemeinen Sinusfunktion (blau) zu sehen. Von diesem sollen nun einige Eigenschaften bestimmt werden. Als Hilfe wurde zusätzlich die Sinuskurve eingezeichnet.
- Gib die Amplitude des Graphen an!
- Gib die Wertemenge an!
- Bestimme die Periode!
- Gib die Nullstellen der Funktion an!
- An welchen Stellen sind die Funktionswerte am kleinsten und wo sind sie am größten?
- Nenne jeweils einen Bereich in dem der Graph streng monoton fallend bzw. steigend ist!
|
|
|
Bestimmung einer Funktionsgleichung aus dem Graphen
|
Merke:
Beachte, zu einem Graphen kann es mehrere zugehörige Funktionsgleichungen geben! D.h., die Antwort auf die Frage nach einer Funktionsgleichung zu einem gegebenen Graphen muss nicht immer eindeutig sein.
Um zu sehen wie man aus dem Graphen einer Funktion eine zugehörige Funktionsgleichung bestimmen kann, klicke hier.
|
|
|
Aufgabe 2 
Bestimme zu folgenden Graphen je einen zugehörigen Funktionsterm der Form 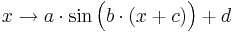 . .
|
|
|
Jetzt noch was zum Knobeln!!!
Aufgabe 3 
- In diesem Applet kannst zu zeigen, ob du zu den gegebenen Graphen den zugehörigen Term findest.
- Gib einen Funktionsterm zu dem Graphen an, den man erhält, falls die Sinuskurve um zwei nach links und um 3 nach oben verschoben wird! Wie lautet die Gleichung, falls zusätzlich die Periode halbiert werden soll?
|
|
|
|
Super! Nun hast du es geschafft und das Ende der zweiten Station erreicht.
Hefteintrag: Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alles Wichtige notiert hast!
Falls du noch etwas üben möchtest, so löse die Zusatzaufgabe!
|
|
Zusatzaufgabe
Aufgabe 4 
In dem unteren Bild sind die Sinuskurve (rot) und ein Graph einer allgemeinen Sinusfunktion (schwarz) zu sehen.
- Du kennst die Nullstellen der Sinusfunktion. Wo sind sie?
- Stelle in der Zeichnung fest, an welchen Stellen der schwarze Graph Nullstellen besitzt und notiere sie!
- Wo hat der Graph der schwarzen Funktion Hochpunkte bzw. Tiefpunkte?
- Wo ist er streng monoton fallend bzw. steigend?
|
|
|
Lösung zu Aufgabe 1
Lösung zu Aufgabe 2:
Hier kannst Du überprüfen, ob deine Ergebnisse stimmen. Stelle dazu die Schieberegler entsprechend ein.
Lösung zu Aufgabe 3
Lösung zu Aufgabe 4
Lösung zu Aufgabe 3: [Anzeigen][Verstecken]
2. Aufgabe:
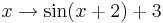
und
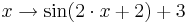
Lösung zu Aufgabe 4: [Anzeigen][Verstecken]
Weiter geht es mit
Station 3: Anwendungen in der Physik
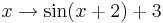 und
und 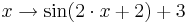
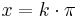 mit
mit  oder
oder 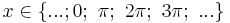
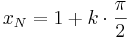 mit
mit  oder
oder 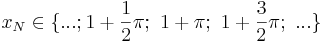
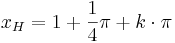 mit
mit  oder
oder 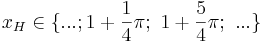
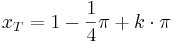 mit
mit  oder
oder 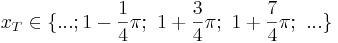
![...;\ [1+\frac{1}{4}\pi;\ 1+\frac{3}{4}\pi];\ [1+\frac{5}{4}\pi;\ 1+\frac{7}{4}\pi];\ ...](/images/math/3/8/c/38cede13d42a4986bf3d2217920545d4.png)
![...;\ [1-\frac{1}{4}\pi;\ 1+\frac{1}{4}\pi];\ [1+\frac{3}{4}\pi;\ 1+\frac{5}{4}\pi];\ ...](/images/math/9/d/1/9d17ad4a42698cc2f951c8cadb0f83ad.png)

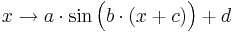 .
.